Modeling infectious disease dynamics: Integrating contact tracing-based stochastic compartment and spatio-temporal risk models

Abstract

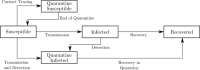
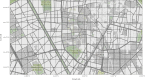
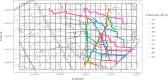
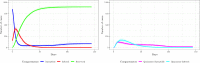
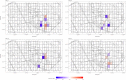
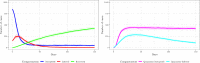
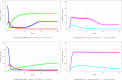
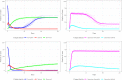
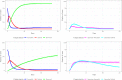
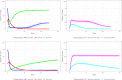
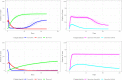
Major infectious diseases such as COVID-19 have a significant impact on population lives and put enormous pressure on healthcare systems globally. Strong interventions, such as lockdowns and social distancing measures, imposed to prevent these diseases from spreading, may also negatively impact society, leading to jobs losses, mental health problems, and increased inequalities, making crucial the prioritization of riskier areas when applying these protocols. The modeling of mobility data derived from contact-tracing data can be used to forecast infectious trajectories and help design strategies for prevention and control. In this work, we propose a new spatial-stochastic model that allows us to characterize the temporally varying spatial risk better than existing methods. We demonstrate the use of the proposed model by simulating an epidemic in the city of Valencia, Spain, and comparing it with a contact tracing-based stochastic compartment reference model. The results show that, by accounting for the spatial risk values in the model, the peak of infected individuals, as well as the overall number of infected cases, are reduced. Therefore, adding a spatial risk component into compartment models may give finer control over the epidemic dynamics, which might help the people in charge to make better decisions.

Keywords: Compartment modeling; Contact tracing; Infectious diseases; Pedestrian mobility; Spatio-temporal modeling.

Fig. 1

Diagram for the base-SIR model with all 5 compartments and the 7 possible transfers.

Fig. 2

Relative Risk (RR) modeling strategy for aggregated contact-tracing data and important covariates.

Fig. 3

Map of the studied part of Valencia city generated using the ggmap package (Kahle and Wickham, 2013) with the previously described 230 overlapped cells.

Fig. 4

Map highlighting in green the 23 selected cells (left), and map highlighting in blue the cells where at least one contact has occurred (right). Red dots represent the buildings. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 5

SUMO simulated trajectories for 10 randomly selected pedestrians in “day 1” in Valencia. “ID #” refers to the pedestrian code number in the data set.

Fig. 6

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR model. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual, as described in Section 3.2.

Fig. 7

Estimated Relative Risks for all 230 cells in the second window of days 1, 2, 3, and 4.

Fig. 8

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the spatio-temporal-SIR model. Light lines represent the 10 realizations of the simulated epidemic, and bold line represents the average number of individual, as described in Section 3.2.

Fig. 9

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR (top) and the spatio-temporal-SIR (bottom) models. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual. Simulation corresponds to scenario 02 from Table 2.

Fig. 10

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR (top) and the spatio-temporal-SIR (bottom) models. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual. Simulation corresponds to scenario 03 from Table 2.

Fig. 11

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR (top) and the spatio-temporal-SIR (bottom) models. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual. Simulation corresponds to scenario 04 from Table 2.

Fig. 12

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR (top) and the spatio-temporal-SIR (bottom) models. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual. Simulation corresponds to scenario 05 from Table 2.

Fig. 13

Number of individuals in each compartment (S, I, R, ${\text{Q}}_{\text{S}}$, and ${\text{Q}}_{\text{I}}$) over the days using the base-SIR (top) and the spatio-temporal-SIR (bottom) models. Light lines represent the 10 realizations of the simulated epidemic, and the bold line represents the average number of individual. Simulation corresponds to scenario 06 from Table 2.