A Fractional-Order Epidemic Model with Quarantine Class and Nonmonotonic Incidence: Modeling and Simulations

Abstract

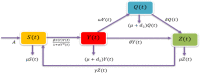
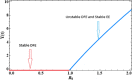
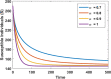
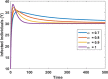
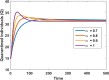
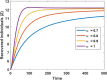
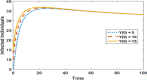
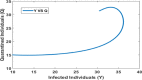
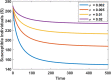
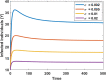
In any outbreak of infectious disease, the timely quarantine of infected individuals along with preventive measures strategy are the crucial methods to control new infections in the population. Therefore, this study aims to provide a novel fractional Caputo derivative-based susceptible-infected-quarantined-recovered-susceptible epidemic mathematical model along with a nonmonotonic incidence rate of infection. A new quarantined individual compartment is incorporated into the susceptible-infected-recovered-susceptible compartmental model by dividing the total population into four subpopulations. The nonmonotonic incidence rate of infection is considered as Monod-Haldane functional type to understand the psychological effects in the population. Qualitative analysis of the study shows that the model solutions are well-posed i.e., they are nonnegative and bounded in an attractive region. It is revealed that the model has two equilibria, namely, disease-free (DFE) and endemic (EE). The stability analysis of equilibria is investigated for local as well as global behaviors. Mathematical analysis of the model reveals that DFE is locally asymptotically stable when the basic reproduction number $\left(R_0\right)$ is lower than one. The basic reproduction number $R_0$ is computed using the next-generation matrix method. The existence of EE is shown and it is investigated that EE is locally asymptotically stable when $R_0>1$ under some appropriate conditions. Moreover, the global stability behaviors of DFE and EE are analyzed under some conditions using $R_0$ . Finally, some numerical simulations are performed to interpret the theoretical findings.

Keywords: Epidemic model; Local and global stabilities; Nonmonotonic incidence rate; Numerical simulation; Quarantine compartment.

Fig. 1

Transfer diagram of the model (4)

Fig. 2

Basic reproduction number $R_0$ versus Infected population $Y(t).$

Fig. 3

Impact of fraction order $\alpha$ on susceptible population

Fig. 4

Impact of fraction order $\alpha$ on infected population

Fig. 5

Impact of fraction order $\alpha$ on quarantine population

Fig. 6

Impact of fraction order $\alpha$ on recovered population

Fig. 7

Impact of different initial values $Y(0)$ on the infected populations at $\alpha =0.8$

Fig. 8

Quarantine population versus infected population at $\alpha =0.8$

Fig. 9

Quarantine population versus recovered population $\alpha =0.8$

Fig. 10

Infected population versus recovered population $\alpha =0.8$

Fig. 11

Impact of psychological effects $(\sigma )$ on the susceptible population at $\alpha =0.8$

Fig. 12

Impact of psychological effects $(\sigma )$ on infected individuals at $\alpha =0.8$