Observation of Rabi dynamics with a short-wavelength free-electron laser

Abstract

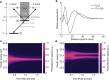
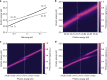
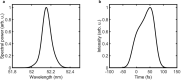
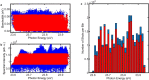
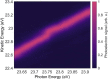
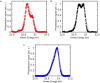
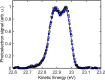
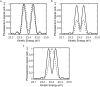
Rabi oscillations are periodic modulations of populations in two-level systems interacting with a time-varying field¹. They are ubiquitous in physics with applications in different areas such as photonics², nano-electronics³, electron microscopy⁴ and quantum information⁵. While the theory developed by Rabi was intended for fermions in gyrating magnetic fields, Autler and Townes realized that it could also be used to describe coherent light-matter interactions within the rotating-wave approximation⁶. Although intense nanometre-wavelength light sources have been available for more than a decade^7-9, Rabi dynamics at such short wavelengths has not been directly observed. Here we show that femtosecond extreme-ultraviolet pulses from a seeded free-electron laser¹⁰ can drive Rabi dynamics between the ground state and an excited state in helium atoms. The measured photoelectron signal reveals an Autler-Townes doublet and an avoided crossing, phenomena that are both fundamental to coherent atom-field interactions¹¹. Using an analytical model derived from perturbation theory on top of the Rabi model, we find that the ultrafast build-up of the doublet structure carries the signature of a quantum interference effect between resonant and non-resonant photoionization pathways. Given the recent availability of intense attosecond¹² and few-femtosecond¹³ extreme-ultraviolet pulses, our results unfold opportunities to carry out ultrafast manipulation of coherent processes at short wavelengths using free-electron lasers.

Fig. 1. Rabi oscillations induced by an XUV-FEL pulse.

a, The sinusoidal energy transfer between the XUV-FEL coupled states $∣a⟩$ and $∣b⟩$ (black horizontal lines) is associated with sign changes of state amplitudes between adjacent Rabi cycles (+ and −). Photoelectrons can be ejected from excited state $∣b⟩$, by one (I) photon, or by two (II) photons from $∣a⟩$ through complement states, $∣c⟩$ (grey horizontal lines). This results in the time-dependent build-up of an ultrafast AT doublet structure. b, The build-up of an ultrafast AT doublet for 1/2, 1 and 3/2 completed Rabi periods is shown for I-photon ionization from $∣b⟩$ (dashed, magenta line) and II-photon ionization from $∣a⟩$ (solid, black line) using the analytical model described in the Supplementary Information. c, Domains of photoionization from 1s²–4p Rabi cycling helium atoms with the dominant photon process: I (red shaded area) and II (blue shaded area). Rabi cycling is limited by spontaneous emission (τ_SE), I-photon ionization from $∣b⟩$ (τ_b) and II-photon ionization from $∣a⟩$ (τ_a) at progressively higher intensities of the FEL field. τ_a+b is the lifetime of the Rabi cycling atom subject to photoionization. The boundary between the two domains is determined by τ_a = τ_b. The diamond marks the experiment: on the boundary between the I and II domains and close to a single Rabi cycle.

Fig. 2. Asymmetry of the ultrafast AT doublet.

a, Deconvoluted experimental photoelectron spectra with a symmetric AT doublet (black squares) at 23.753-eV photon energy, and the asymmetric ones at ±13-meV detuning (blue diamonds and red circles, respectively). b, Ab initio photoelectron spectra using TDCIS at three photon energies with a symmetric AT doublet at 24.157-eV photon energy (dashed black line) and the asymmetric ones at ±13-meV detuning. The red (blue) curve corresponds to red (blue) detuned light. c,d, The same as in b, but using the analytical model for 3/2 Rabi periods in the case of one-photon ionization from $∣b⟩$ (c) and two-photon ionization from $∣a⟩$ (d). The loss of contrast observed in the experimental spectra arises owing to macroscopic averaging of the target gas sample (see Supplementary Information for details). a.u., arbitrary units.

Fig. 3. Quantum interference with a giant wave.

a, Energy-level diagram for the photon transitions that lead to quantum interference. b, The summation of contributions from the non-resonant (grey) states in a leads to the formation of a giant wave, $∣{\rho }_{\ne b}⟩$. The excited state $∣b⟩$ is shown for comparison with a magnification factor of 10 (dotted black line). Both wavefunctions are computed for helium using CIS. c, Photoelectron spectra from the total analytical model containing contributions from both ground $∣a⟩$ and excited $∣b⟩$ states with resonant atomic excitation Δω = 0. d, The same as in c, but with Δω = 62 meV. The dashed white lines denote the expected kinetic energy (23.3076 eV) of a photoelectron that has absorbed two resonant photons. a.u., arbitrary units.

Fig. 4. Avoided crossing phenomena in the energy domain.

a, Photoelectron kinetic energies, for one photon above the energy of the dressed-atom states, as a function of detuning. b–d, Photoelectron spectra as a function of the photon energy retrieved experimentally (b), using TDCIS (c) and using the total analytical model for 3/2 Rabi periods (d). In each case, the dashed white line corresponds to the photon energy for the 1s² → 1s4p transition in helium. The shifts between the energy scales of a and b, and the energy scales of c and d, are due to the difference between the experimental and the Hartree–Fock ionization potential. a.u., arbitrary units.

Extended Data Fig. 1. Simulated FEL pulse properties.

a,b, Spectral (a) and temporal (b) profiles of the XUV-FEL pulse as obtained from the simulations using PERSEO.

Extended Data Fig. 2. Filtering criteria for the measured data.

a, Shot-to-shot variation of the FEL bandwidth (FWHM) as a function of the photon energy. The blue dots represent the measured FWHM using the PADRES spectrometer and the red dots represent the filtered shots. b, Same as a, but for the integrated spectral intensity. c, All the shots are distributed over 30 equally spaced (spacing: ~13 meV) photon-energy bins, spanning the entire range of wavelength scan. The red ones correspond to the filtered shots satisfying both the criteria in panel a–b.

Extended Data Fig. 3. Avoided crossing without deconvolution.

Measured photoelectron spectra, as a function of the photon energy, without any deconvolution procedure performed. Notice the faint avoided crossing.

Extended Data Fig. 4. Experimental photoelectron spectra with and without deconvolution.

a, Experimental photoelectron spectra at 23.740 eV photon energy. Solid line: raw data and circles: deconvoluted form. b, Same as a, but at 23.753 eV photon energy. Here, the solid line represents the raw data and the squares represent the deconvoluted spectrum. c, Same as a–b, but at 23.766 eV photon energy, where once again the solid line constitutes the raw data and the diamonds are for its deconvoluted form. In each case, the open symbols are same as shown in Fig. 2a of the main text. The shaded region in each sub-panel represents the corresponding Poisson fluctuations of the photoelectron signal.

Extended Data Fig. 5. Deconvoluted spectra with two different filtering criteria.

Deconvoluted experimental photoelectron spectra at 23.753 eV for two different filtering criteria. Open black squares: for photon bandwidth of 20–65 meV and integrated spectral intensity of 0.8 × 10⁵ – 1.6 × 10⁵ (same as in the Fig. 2a of main text). Solid blue line: for photon bandwidth of 1–45 meV and integrated spectral intensity of 1 × 10⁵–3 × 10⁵.

Extended Data Fig. 6. Effects of intensity averaging on the photoelectron spectrum.

a, Photoelectron spectra generated with the analytic model for a single atom (solid line), and for a macroscopic sample (dashed line). A pulse length of 3/2 Rabi periods, and detuning of Δω = 62 meV was used. b-c, Same as a, but for the individual contributions of the two- and one-photon processes, respectively. The results in both b, and c are calculated for Δω = 0 meV, where the spectra are symmetric. The separate contributions are normalized to the maximum of the one-photon spectra for both the single-atom and intensity averaged signals.