TreeKnit: Inferring ancestral reassortment graphs of influenza viruses
- PMID: 35984845
- PMCID: PMC9447925
- DOI: 10.1371/journal.pcbi.1010394
TreeKnit: Inferring ancestral reassortment graphs of influenza viruses
Abstract
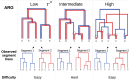
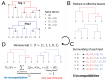
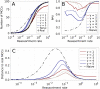
When two influenza viruses co-infect the same cell, they can exchange genome segments in a process known as reassortment. Reassortment is an important source of genetic diversity and is known to have been involved in the emergence of most pandemic influenza strains. However, because of the difficulty in identifying reassortment events from viral sequence data, little is known about their role in the evolution of the seasonal influenza viruses. Here we introduce TreeKnit, a method that infers ancestral reassortment graphs (ARG) from two segment trees. It is based on topological differences between trees, and proceeds in a greedy fashion by finding regions that are compatible in the two trees. Using simulated genealogies with reassortments, we show that TreeKnit performs well in a wide range of settings and that it is as accurate as a more principled bayesian method, while being orders of magnitude faster. Finally, we show that it is possible to use the inferred ARG to better resolve segment trees and to construct more informative visualizations of reassortments.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


Similar articles
-
Bayesian inference of reassortment networks reveals fitness benefits of reassortment in human influenza viruses.Proc Natl Acad Sci U S A. 2020 Jul 21;117(29):17104-17111. doi: 10.1073/pnas.1918304117. Epub 2020 Jul 6. Proc Natl Acad Sci U S A. 2020. PMID: 32631984 Free PMC article.
-
A phylogenetic approach to detecting reassortments in viruses with segmented genomes.Gene. 2010 Sep 15;464(1-2):11-6. doi: 10.1016/j.gene.2010.05.002. Epub 2010 May 28. Gene. 2010. PMID: 20546849
-
New approaches for unravelling reassortment pathways.BMC Evol Biol. 2013 Jan 1;13:1. doi: 10.1186/1471-2148-13-1. BMC Evol Biol. 2013. PMID: 23279962 Free PMC article.
-
Progress and Challenge in Computational Identification of Influenza Virus Reassortment.Virol Sin. 2021 Dec;36(6):1273-1283. doi: 10.1007/s12250-021-00392-w. Epub 2021 May 26. Virol Sin. 2021. PMID: 34037948 Free PMC article. Review.
-
[The pandemic influenza virus H1N1/2009: a review of the molecular biology, phylogeny, history of reassortments, and parameters of host switching].Bundesgesundheitsblatt Gesundheitsforschung Gesundheitsschutz. 2010 Dec;53(12):1231-7. doi: 10.1007/s00103-010-1166-0. Bundesgesundheitsblatt Gesundheitsforschung Gesundheitsschutz. 2010. PMID: 21161472 Review. German.
Cited by
-
Concepts and Methods for Predicting Viral Evolution.Methods Mol Biol. 2025;2890:253-290. doi: 10.1007/978-1-0716-4326-6_14. Methods Mol Biol. 2025. PMID: 39890732
-
Dimensionality reduction distills complex evolutionary relationships in seasonal influenza and SARS-CoV-2.bioRxiv [Preprint]. 2024 Aug 29:2024.02.07.579374. doi: 10.1101/2024.02.07.579374. bioRxiv. 2024. Update in: Virus Evol. 2024 Nov 14;10(1):veae087. doi: 10.1093/ve/veae087. PMID: 39253501 Free PMC article. Updated. Preprint.
-
The Number and Pattern of Viral Genomic Reassortments are not Necessarily Identifiable from Segment Trees.Mol Biol Evol. 2024 Jun 1;41(6):msae078. doi: 10.1093/molbev/msae078. Mol Biol Evol. 2024. PMID: 38648521 Free PMC article.
-
Using homologous network to identify reassortment risk in H5Nx avian influenza viruses.PLoS Comput Biol. 2025 Jul 22;21(7):e1013301. doi: 10.1371/journal.pcbi.1013301. eCollection 2025 Jul. PLoS Comput Biol. 2025. PMID: 40694591 Free PMC article.
-
Concepts and methods for predicting viral evolution.bioRxiv [Preprint]. 2024 Nov 30:2024.03.19.585703. doi: 10.1101/2024.03.19.585703. bioRxiv. 2024. Update in: Methods Mol Biol. 2025;2890:253-290. doi: 10.1007/978-1-0716-4326-6_14. PMID: 38746108 Free PMC article. Updated. Preprint.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

