Wing Kinematics and Unsteady Aerodynamics of a Hummingbird Pure Yawing Maneuver

Abstract

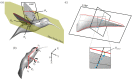
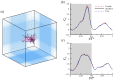
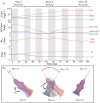
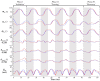
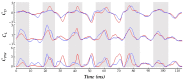
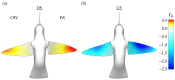
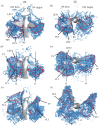
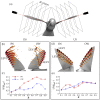
As one of few animals with the capability to execute agile yawing maneuvers, it is quite desirable to take inspiration from hummingbird flight aerodynamics. To understand the wing and body kinematics and associated aerodynamics of a hummingbird performing a free yawing maneuver, a crucial step in mimicking the biological motion in robotic systems, we paired accurate digital reconstruction techniques with high-fidelity computational fluid dynamics (CFD) simulations. Results of the body and wing kinematics reveal that to achieve the pure yaw maneuver, the hummingbird utilizes very little body pitching, rolling, vertical, or horizontal motion. Wing angle of incidence, stroke, and twist angles are found to be higher for the inner wing (IW) than the outer wing (OW). Unsteady aerodynamic calculations reveal that drag-based asymmetric force generation during the downstroke (DS) and upstroke (US) serves to control the speed of the turn, a characteristic that allows for great maneuvering precision. A dual-loop vortex formation during each half-stroke is found to contribute to asymmetric drag production. Wake analysis revealed that asymmetric wing kinematics led to leading-edge vortex strength differences of around 59% between the IW and OW. Finally, analysis of the role of wing flexibility revealed that flexibility is essential for generating the large torque necessary for completing the turn as well as producing sufficient lift for weight support.

Keywords: bio-inspired maneuvering performance; computational fluid dynamics simulation; hummingbird pure yaw maneuver.

Figure 1

(a) Hummingbird skeleton and Catmull–Clark subdivisions superimposed on the real hummingbird; (b) fully rigged hummingbird model with skin surface; illustration of the hummingbird yaw turn at 3 time instances (c) 1 ms; (d) 26 ms; (e) 54 ms.

Figure 2

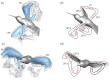
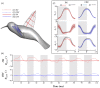
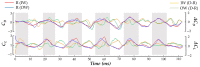
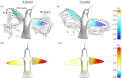
(a) Illustration of the wing kinematics angles of stroke Ψ_w, deviation θ_w, and pitch Φ_w. The wing root-to-tip vector is shown as a dotted red line, the wing leading-edge to trailing-edge vector is shown as a dotted red line on the opposing wing; (b) Visualization of the body coordinate system with global reference frame pictured; (c) LSRP rendering with definition of θ_twist as the angle between the wing and the least deformed wing plane.

Figure 3

(a) Computational domain illustrating the orientation of the body in the fluid domain, (b) comparison of the forces for the inner wing and (c) outer wing for the coarse mesh (~7.1 million grids), medium mesh (~11.2 million grids), and fine mesh (~17.0 million grids).

Figure 4

Summary of the body kinematics of the hummingbird including (a) body Euler angles, root squared error of the body Euler angles relative to the mean, plot of yaw angular velocity, and body horizontal (H) and vertical (V) displacements as well as (b) visualization of the yaw turn.

Figure 5

Wingbeat kinematics variables of stroke (Ψ_w), deviation (θ_w), angle of incidence (Φ_w), θ_twist at 0.25 R, 0.50 R, and 0.75 R, and wing tip velocity (U_tip) during the entire maneuvering motion. DS is indicated by grey shading and US is indicated by white shading. IW is indicated by red curves and OW is indicated by blue curves. R represents span length.

Figure 6

Time series comparison of the normalized drag, lift, and power consumption by the inner (red) and outer (blue) wing.

Figure 7

(a) Phase II, ‘turning phase’, average DS and (b) average US non-dimensional drag forces produced by the wings.

Figure 8

Wake topology generated by the hummingbird’s third DS at (a) t/T* = 0.16, (b) t/T* = 0.32, and (c) t/T* = 0.48 and third stroke US at (d) t/T* = 0.60, (e) t/T* = 0.72, and (f) t/T* = 0.98. The lines labelled s1 and s2 in (b,e) denote the slices that the data in Figure 9 are shown on.

Figure 9

Comparison of wake jets for the IW (a,c), OW (b,d) during the DS and US, respectively.

Figure 10

(a) Schematic of camera placement for computing the 2D spanwise slice cuts; (b) IW and OW vorticity contours at peak DS force production with (c) corresponding $\Gamma$, normalized by average U_tipc; (d,e) represent the same information as (b,c) but for the US.

Figure 11

(a) Pressure iso-surface with (b) associated vortex structures generated during the DS; (c,d) represent the same information as (a,b) but for the US.

Figure 12

(a) Comparison of the deforming (dotted lines) and rigid (solid lines) wing models through tracking the chord lines at different span lengths; (b) quantitative comparison of IW and OW θ_twist for the deforming and rigid models; (c) comparison of the R and D model wing kinematics of stroke (Ψ_w), deviation (θ_w), angle of incidence (Φ_w).

Figure 13

Drag and lift coefficient production comparison for the R model, with red indicating IW and blue indicating OW. The left-hand side y-axis represents the R model force coefficients, while the right-hand side y-axis represents the difference between the D and R model.

Figure 14

R model (a) surface pressure contours with pressure iso-surfaces at stroke 3 t/T* = 0.32 with corresponding (b) drag force production. (c,d) represent the same information for the F model.