A statistical mechanics model for determining the length distribution of actin filaments under cellular tensional homeostasis

Abstract

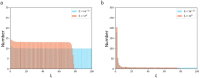
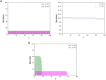
Tensional homeostasis is a cellular process whereby nonmuscle cells such as fibroblasts keep a constant level of intracellular tension and signaling activities. Cells are allowed thanks to tensional homeostasis to adapt to mechanical stress, but the detailed mechanism remains unclear. Here we address from a theoretical point of view what is required for maintaining cellular tensional homeostasis. A constrained optimization problem is formulated to analytically determine the probability function of the length of individual actin filaments (AFs) responsible for sustaining cellular tension. An objective function composed of two entropic quantities measuring the extent of formation and dispersion of AFs within cells is optimized under two constraint functions dictating a constant amount of actin molecules and tension that are arguably the two most salient features of tensional homeostasis. We then derive a specific probability function of AFs that is qualitatively consistent with previous experimental observations, in which short AF populations preferably appear. Regarding the underlying mechanism, our analyses suggest that the constraint for keeping the constant tension level makes long AF populations smaller in number because long AFs have a higher chance to be involved in bearing larger forces. The specific length distribution of AFs is thus required for achieving the constrained objectives, by which individual cells are endowed with the ability to stably maintain a homeostatic tension throughout the cell, thereby potentially allowing cells to locally detect deviation in the tension, keep resulting biological functions, and hence enable subsequent adaptation to mechanical stress. Although minimal essential factors are included given the actual complexity of cells, our approach would provide a theoretical basis for understanding complicated homeostatic and adaptive behavior of the cell.

Figure 1

Schematic to explain $S_d$. (a) Schematic of the cytoplasm (black) where AFs (green) assumed to be formed by one-dimensional association of actin monomers to have a length of $l_{\text{i}}$ are spatially distributed. (b) The cytoplasm is divided by compartments with a length of $\text{a}$. AFs (green) occupy some of the compartments (gray). The arrows in the cell show the length of AFs. An example of $l_{\text{i}}$ comprising of 15 actin monomers is shown. See Supporting Material for detailed explanation.

Figure 2

Length distribution of AFs comprising of $\text{N}$ = 1,000 monomers at ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 1 (a), ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 2 (b), ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 4 (c), ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 6 (d), ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 8 (e), and ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 10 (f). With a larger ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$, populations of AFs with shorter lengths increase in the cell.

Figure 3

Length distribution of AFs comprising of $\text{N}$ = 1000 monomers with $f_0$ = 10^–12 (blue) and $f_0$ = 1 (orange) at ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 0.1 (a) and ${\text{k}}_{\text{b}}^{\prime }/{\text{k}}_{\text{b}}$ = 4 (b).

Figure 4

Length distribution of AFs comprising of $\text{N}$ = 1000 monomers at $f_0$ = 10^–6 (a), $f_0$ = 10^–4 (b), $f_0$ = 10^–2 (c), and $f_0$ = 10⁰ (d).

Figure 5

Length distribution of AFs comprising of $\text{N}$ = 1000 monomers with $l_0$ = 20 (green) and $l_0$ = 80 (pink) at $f_0$ = 10^–4 (a) and $f_0$ = 10⁰ (b). For visual clarity, point plots are also shown on the right for the case of a with magnified vertical axis.