A prevalence-based transmission model for the study of the epidemiology and control of soil-transmitted helminthiasis
- PMID: 36006929
- PMCID: PMC9409602
- DOI: 10.1371/journal.pone.0272600
A prevalence-based transmission model for the study of the epidemiology and control of soil-transmitted helminthiasis
Abstract
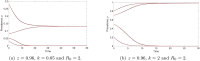
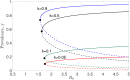
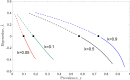
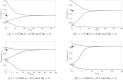
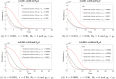
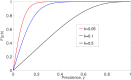
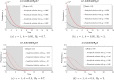
Much effort has been devoted by the World Health Organization (WHO) to eliminate soil-transmitted helminth (STH) infections by 2030 using mass drug administration targeted at particular risk groups alongside the availability to access water, sanitation and hygiene services. The targets set by the WHO for the control of helminth infections are typically defined in terms of the prevalence of infection, whereas the standard formulation of STH transmission models typically describe dynamic changes in the mean-worm burden. We develop a prevalence-based deterministic model to investigate the transmission dynamics of soil-transmitted helminthiasis in humans, subject to continuous exposure to infection over time. We analytically determine local stability criteria for all equilibria and find bifurcation points. Our model predicts that STH infection will either be eliminated (if the initial prevalence value, y(0), is sufficiently small) or remain endemic (if y(0) is sufficiently large), with the two stable points of endemic infection and parasite eradication separated by a transmission breakpoint. Two special cases of the model are analysed: (1) the distribution of the STH parasites in the host population is highly aggregated following a negative binomial distribution, and (2) no density-dependent effects act on the parasite population. We find that disease extinction is always possible for Case (1), but it is not so for Case (2) if y(0) is sufficiently large. However, by introducing stochastic perturbation into the deterministic model, we discover that chance effects can lead to outcomes not predicted by the deterministic model alone, with outcomes highly dependent on the degree of worm clumping, k. Specifically, we show that if the reproduction number and clumping are sufficiently bounded, then stochasticity will cause the parasite to die out. It follows that control of soil-transmitted helminths will be more difficult if the worm distribution tends towards clumping.
Conflict of interest statement
The authors have declared that no competing interests exist.
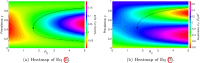
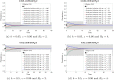
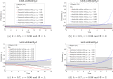
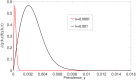
Figures





Similar articles
-
The 'breakpoint' of soil-transmitted helminths with infected human migration.J Theor Biol. 2020 Feb 7;486:110076. doi: 10.1016/j.jtbi.2019.110076. Epub 2019 Nov 13. J Theor Biol. 2020. PMID: 31733259 Free PMC article.
-
Baseline patterns of infection in regions of Benin, Malawi and India seeking to interrupt transmission of soil transmitted helminths (STH) in the DeWorm3 trial.PLoS Negl Trop Dis. 2020 Nov 2;14(11):e0008771. doi: 10.1371/journal.pntd.0008771. eCollection 2020 Nov. PLoS Negl Trop Dis. 2020. PMID: 33137100 Free PMC article.
-
Association between water, sanitation, and hygiene access and the prevalence of soil-transmitted helminth and schistosome infections in Wolayita, Ethiopia.Parasit Vectors. 2022 Nov 4;15(1):410. doi: 10.1186/s13071-022-05465-7. Parasit Vectors. 2022. PMID: 36333779 Free PMC article.
-
Interventions to improve disposal of child faeces for preventing diarrhoea and soil-transmitted helminth infection.Cochrane Database Syst Rev. 2019 Sep 24;9(9):CD011055. doi: 10.1002/14651858.CD011055.pub2. Cochrane Database Syst Rev. 2019. PMID: 31549742 Free PMC article.
-
Why Are We Still a Worm World in the 2020s? An Overview of Risk Factors and Endemicity for Soil-Transmitted Helminthiasis.Acta Parasitol. 2023 Sep;68(3):481-495. doi: 10.1007/s11686-023-00701-1. Epub 2023 Aug 2. Acta Parasitol. 2023. PMID: 37531011 Review.
Cited by
-
Bartonella infections are prevalent in rodents despite efficient immune responses.Parasit Vectors. 2023 Sep 4;16(1):315. doi: 10.1186/s13071-023-05918-7. Parasit Vectors. 2023. PMID: 37667323 Free PMC article.
-
Progress and challenges for the application of machine learning for neglected tropical diseases.F1000Res. 2025 Jul 17;12:287. doi: 10.12688/f1000research.129064.3. eCollection 2023. F1000Res. 2025. PMID: 40642109 Free PMC article. Review.
-
A scoping review of transmission models for soil-transmitted helminth infections to underpin the development of a transmission model for Strongyloides stercoralis.Parasitology. 2024 Dec;151(14):1508-1521. doi: 10.1017/S0031182024001392. Parasitology. 2024. PMID: 39545321 Free PMC article.
References
-
- Soil-transmitted helminth infections, Tech. rep., World Health Organization (2019). URL https://www.who.int/news-room/fact-sheets/detail/soil-transmitted-helmin...
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

