Solitonic Windkessel Model for Intracranial Aneurysm

Abstract

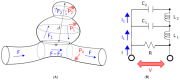
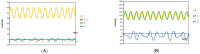
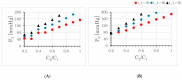
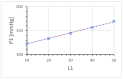
The Windkessel model, which is known as a successful model for explaining the hemodynamic circulation, is a mathematical model with a direct correspondence with the electric circuit. We propose a theoretical model for the intracranial aneurysm based on the Windkessel-type steady blood flow. Intracranial aneurysms are well known vascular lesions, which cause subarachnoid hemorrhages. Since an aneurysm is an end-sack formed on the blood vessel, it functions as an unusual blood path that has characteristic features such as a reservoir and bottle neck orifice. We simulate an aneurysm by an electric circuit consisting of three different impedances, resistance, capacitance and inductance. A dumbbell-shaped aneurysm is the most dangerous aneurysm to easily rupture. Our aneurysmal model is created as a two-story aneurysm model for this point, thus namely the five-element Windkessel. Then, the mathematical formula was solved in numerical simulations by changing the size of the aneurysm and the elasticity of the aneurysm wall. An analysis of this model provided that the presence of the daughter aneurysm and the thinning of the aneurysm wall are positively correlated with a sharp increase in blood pressure in the aneurysm dome. Our mathematic aneurysm model proposes a good analogue to the real aneurysm and proved that this model includes soliton that is a non-decreasing wave propagation.

Keywords: Windkessel model; intracranial aneurysm; soliton; subarachnoid hemorrhage.

Figure 1

(A) Doubly composed intracranial aneurysm consisting of mother and daughter aneurysms (also called dumbbell-shaped aneurysm in the preceding works). The blood flow F is the amount of blood flow pumping from the heart, F₁ is the blood flow in the mother aneurysm and F₂ is the blood flow in the daughter aneurysm, where the circulative flows with the opposite direction are assumed in the aneurysms. (B) Solitonic Windkessel model for the doubly composed intracranial aneurysm. The corresponding electric circuit is shown, where C₁ and C₂ corresponds to the size/dimension of mother and daughter aneurysms, respectively. R determines the branching ratio F₁ = F of the blood flow. The constants L₁ and L₂ are related to the elasticity of blood vessel wall. P₀, P₁ and P₂ denote the local pressures, and F, F₁, and F₂ are blood flows.

Figure 2

Blood flow F(t) and blood pressure P(t) in the main vessel are given in the left panel (A) and the right panel (B), respectively. Environmental variables are determined by the heartbeat: blood pressure P(t) and blood flow F(t) are plotted for 0–20 s. These are regularly provided by the heart. The time periodic oscillation is fixed by the typical beat 70 bpm (Table 1), the blood pressure is assumed to range from 80 to 120 mmHg and the blood flow to be 40 to 60 mL/min.

Figure 3

(A) The branching of blood flow from F(t) to F₁(t) and F₂(t) at a given setting (R = 2.2, C₁ = 0.100, C₂ = 0.005 and L₁ = 10, L₂ = 20). Here, we take R = 2.2 for the local blood flow in the main vessel F–F₁ not to change too much (less than 10% in all the calculated cases) compared to F. It simulates the typical case of doubly composed aneurysm. Calculation shows that the blood flow in the artery F is almost equal to the blood flow in the parent artery F–F₁, and therefore the blood flows in the aneurysms are kept to be small. Depending on the choice of four parameters (C₁, C₂, L₁, and L₂), flows F₁ and F₂ can be either positive, zero or negative. (B) In the same parameter setting, the local pressures P₁(t) and P₂(t) are calculated, which note that the blood pressure at the parent artery is equal to P(t) regardless of the choice of parameter. In this parameter setting, the amplitude of local pressure P₁(t) is almost equal to P(t), while another local pressure P₂(t) oscillates with irregular beat and small amplitude.

Figure 4

Maximum value of local blood pressure P₂ depending on the size of daughter aneurysms. By fixing the size parameter C₁ of mother aneurysm, the size ratio between mother and daughter aneurysms is changed as C₂/C₁ = 0.20, 0.30, … 1.00 for a fixed C₁ = 0.10. C₂/C₁ = 1.00 corresponds to the ideal dumbbell shape. Note that the blood flow and blood pressure in the artery are almost unchanged (yellow and red ones in Figure 3), while local flows F₁ and F₂ and local pressures P₁ and P₂ easily change their maximum amplitude depending on the parameter. For the growth of daughter aneurysm, an ordinary scenario with L₁ = 2L₂ is demonstrated in the left panel (A), and a solitonic scenario with L₁ = L₂ is demonstrated in the right panel (B) (cf. Section 2.2). In all the presented cases, P₁ is no more than 170 mmHg.

Figure 5

Maximum value of the local blood pressure P₁ depending on the aneurysmal compliance L₁. The daughter aneurysms are not assumed to be formed well (C₂ = 0.1, C₂ = 0.001, L₂ = 0). By changing the compliance parameter L₁ of mother aneurysm, the local pressure P₁ of mother aneurysm increases linearly. Note that the blood flow F–F₁ and blood pressure P in the parent artery is nothing different from those given by Figure 3.

Figure 6

Blood flow (A) and blood pressure (B) at a given setting (R = 2.2, C₁ = 0.100, C₂ = 0.100 and L₁ = 30, L₂ = 60). Although the amplitude of resonating pressure |P₂| becomes large, the resonating flow F₂ is kept to be small enough to be less than 10 mL/min.