Enhancing Mixing Performance in a Rotating Disk Mixing Chamber: A Quantitative Investigation of the Effect of Euler and Coriolis Forces

Abstract

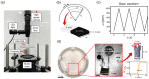
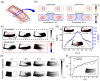
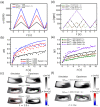
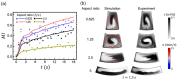
Lab-on-a-CD (LOCD) is gaining importance as a diagnostic platform due to being low-cost, easy-to-use, and portable. During LOCD usage, mixing and reaction are two processes that play an essential role in biochemical applications such as point-of-care diagnosis. In this paper, we numerically and experimentally investigate the effects of the Coriolis and Euler forces in the mixing chamber during the acceleration and deceleration of a rotating disk. The mixing performance is investigated under various conditions that have not been reported, such as rotational condition, chamber aspect ratio at a constant volume, and obstacle arrangement in the chamber. During disk acceleration and deceleration, the Euler force difference in the radial direction causes rotating flows, while the Coriolis force induces perpendicular vortices. Increasing the maximum rotational velocity improves the maximum rotational displacement, resulting in better mixing performance. A longer rotational period increases the interfacial area between solutions and enhances mixing. Mixing performance also improves when there is a substantial difference between Euler forces at the inner and outer radii. Furthermore, adding obstacles in the angular direction also passively promotes or inhibits mixing by configuration. This quantitative investigation provides valuable information for designing and developing high throughput and multiplexed point-of-care LOCDs.

Keywords: Coriolis force; Euler force; microfluidics; mixing; rotating disk.

Figure 1

(a) Experimental setup; the 3D printed disk is rotated by the BLDC motor. The 3D-printed coupling was used to link the BLDC motor and the 3D-printed disk chip to the motor. A high-speed camera with a zoom lens and an LED light was used to capture the mixing process. (b) Schematic of the rotational mixing chamber, where, $r_i$ and $r_o$ are the inner and outer radii of the chamber, respectively. Here, $w$ is the radial width of the chamber, $\ell$ is the arc length of the midpoint of the outer and inner radii, and $h$ is the height of the chamber. Initially, the chamber contained a 0.1 wt.% of dye solution and DI water. (c) As a basic rotational condition, the rotational velocity (ω) and period were set as a triangular waveform with a maximum ω of 1000 rpm, a period of 3 s, and a total of 6 cycles. (d) The series of rotational type mixers in a disk and the magnification of the chamber mixer. The two different solutions were initially placed in the chamber using inlets 1 and 2, the outlet, and three mechanical valves. $d_i$ and $d_o$ are inlet and outlet reservoir diameters for gentle injection using capillary pressure. After injecting each solution, the inlets and outlet were closed by rotating the screw valve. Before mixing, the solution showed a sharp interface between the dye and DI water, and the interfacial thickness ($\delta$) was measured to be ~1.4 mm.

Figure 2

Simulation and experiment results when the rotational velocity $\omega$ was varied as a triangular waveform from 0 to 1000 rpm every 3 s. (a) Simulation result showing 3D streamlines in the chamber. (b) The Coriolis force and the streamlines at 0.5 s and 2.5 s at the cross-sectional mid-plane (blue dashed line in (a)). (c) Concentration and velocity vectors at the horizontal mid-plane during acceleration and deceleration. (d) Angular displacement ($\Delta \varphi$) and rotational velocity ($\omega$) with time. The term $\Delta \varphi$ indicates the angle, measuring the angular displacement between the initial and leading interfaces of the solutions. (e) Comparison of mixing behaviors between the simulation and experiment. (f) Mixing index for simulation (solid line), experiment (dots), and the image of simulation at 18 s of mixing where MI = 0.51 (inset).

Figure 3

Mixing behaviors with various rotational conditions. Case 1 (a–c): (a) Triangular waveform of rotational velocity of $\omega$ for maximum speeds of 1000, 2000, and 3000 rpm with a constant period of 3 s. (b) Mixing index for the simulation (solid line) and experiment (dots), with the conditions of (a). (c) Concentration comparison between the simulation and experiment at 1.5 s for the maximum rpm of 1000, 2000, and 3000 rpm. The arrows in the simulation images depict the velocity vectors. Case 2 (d–f): (d) Triangular waveform for the rotational periods of 1, 2, 3, and 6 s with maximum angular velocities of 333, 667, 1000, and 2000 rpm, respectively. (e) Mixing index for the simulation (solid line) and experiment (dots), with the conditions of (d). (f) Concentration comparison between the simulation and experiment at 3 s for rpm_max = 667 with a period of 2 s and rpm_max = 2000 with a period of 6 s.

Figure 4

(a) Mixing index of the concentration for the simulation (solid line) and experiment (dots), with time for various aspect ratios ($\ell /w$) of the chamber. (b) Flow visualization of the chamber for both simulation and experiment at $t=1.5 \mathrm{s}$.

Figure 5

(a) Schematic of a rotating mixing chamber with five square pillars of 0.5 (w)$\times$0.5 (w)$\times$1 (h) ${\mathrm{mm}}^3$. Here, $d_{\mathsf{\theta }}$ and $d_{\mathrm{r}}$ are the distances between the pillars in angular and radial directions, respectively. The five pillars from 1 to 5 were fabricated using a 3D printer, as seen in the side-cut image. (b) Flow visualization of the chamber for both the simulation and experiment at $d_{\mathsf{\theta }}$:$d_{\mathrm{r}}$ of (i) 1.0 mm:0 mm, (ii) 2.0 mm:0 mm, and (iii) 2.0 mm:3.0 mm at $t$ = 1.5 s. (c) The mixing index for the simulation (solid line) and experiment (dots) with varying $d_{\mathsf{\theta }}$ at fixed $d_{\mathrm{r}}=0 \mathrm{mm}$. (d) Comparison of the mixing index at t = 18 s based on the simulation with and without pillars for different values of $d_{\mathsf{\theta }}$. (e) The mixing index of the simulation (solid line) and experiment (dots) with varying $d_{\mathrm{r}}$ at fixed $d_{\mathsf{\theta }}$ of 2.0 mm. (f) Comparison of mixing index at t = 18 s based on simulation with and without pillars at various values of $d_{\mathrm{r}}$.