Poincaré Plot Nonextensive Distribution Entropy: A New Method for Electroencephalography (EEG) Time Series

Abstract

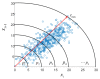
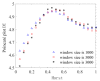
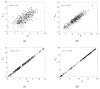
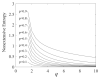
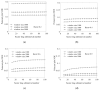
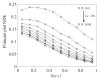
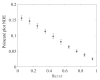
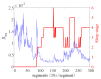
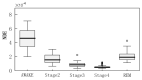
As a novel form of visual analysis technique, the Poincaré plot has been used to identify correlation patterns in time series that cannot be detected using traditional analysis methods. In this work, based on the nonextensive of EEG, Poincaré plot nonextensive distribution entropy (NDE) is proposed to solve the problem of insufficient discrimination ability of Poincaré plot distribution entropy (DE) in analyzing fractional Brownian motion time series with different Hurst indices. More specifically, firstly, the reasons for the failure of Poincaré plot DE in the analysis of fractional Brownian motion are analyzed; secondly, in view of the nonextensive of EEG, a nonextensive parameter, the distance between sector ring subintervals from the original point, is introduced to highlight the different roles of each sector ring subinterval in the system. To demonstrate the usefulness of this method, the simulated time series of the fractional Brownian motion with different Hurst indices were analyzed using Poincaré plot NDE, and the process of determining the relevant parameters was further explained. Furthermore, the published sleep EEG dataset was analyzed, and the results showed that the Poincaré plot NDE can effectively reflect different sleep stages. The obtained results for the two classes of time series demonstrate that the Poincaré plot NDE provides a prospective tool for single-channel EEG time series analysis.

Keywords: Poincaré plot; distribution entropy; nonextensive; sector ring subinterval.

Figure 1

Schematic diagram of Poincaré plot sector ring subintervals. The blue ones are scatter points, the black ones are concentric arcs and the red rays are the maximum distance from the scattered point to the origin.

Figure 2

Poincaré plot DE analysis results of fractional Brownian motion time series with different Hurst indices when the window lengths are 1000, 3000, and 5000.

Figure 3

The Poincaré plots of fractional Brownian motion time series (a) when Hurst exponent is 0.1; (b) when Hurst exponent is 0.3; (c) when Hurst exponent is 0.7; (d) when Hurst exponent is 0.9.

Figure 4

The corresponding relationship between the NE and the nonextensive parameter $$q$$ when probability $$p$$ takes different values.

Figure 5

When the sliding time window widths are 1000, 3000, and 5000, the corresponding relationship between the Poincaré plot NDE of the fractional Brownian motion time series and the number of sector ring subintervals changes continuously. (a) Hurst index is 0.2; (b) Hurst index is 0.4; (c) Hurst index is 0.6; (d) Hurst index is 0.9.

Figure 6

Under different window widths (W.W), the Hurst indices of the fractional Brownian motion time series corresponds to the Poincaré plot NDE.

Figure 7

After the parameters are determined, Poincaré plot NDE mean and standard deviation for different Hurst indices corresponding to fractional Brownian motion time series.

Figure 8

Comparison chart of sleep stage and Poincaré plot NDE analysis results of subjects sc4002e0; red step line is sleep stage and blue curve is Poincaré plot NDE. The red curve indicates different sleep stages.

Figure 9

Multi-independent samples nonparametric Jonckheere–Terpstra test boxplots of NDE analysis results for 5 brain states.