Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Aug 9:16:932270.
doi: 10.3389/fnins.2022.932270. eCollection 2022.

An energy-efficient in-memory computing architecture for survival data analysis based on resistive switching memories

Andrea Baroni  1 , Artem Glukhov  2 , Eduardo Pérez  1 , Christian Wenger  1   3 , Enrico Calore  4   5 , Sebastiano Fabio Schifano  5   6 , Piero Olivo  7 , Daniele Ielmini  2 , Cristian Zambelli  7
Affiliations

An energy-efficient in-memory computing architecture for survival data analysis based on resistive switching memories

Andrea Baroni et al. Front Neurosci. .

Abstract

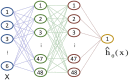
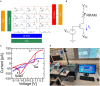
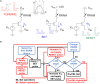
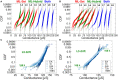
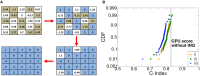
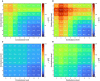
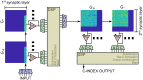
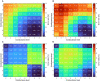
One of the objectives fostered in medical science is the so-called precision medicine, which requires the analysis of a large amount of survival data from patients to deeply understand treatment options. Tools like machine learning (ML) and deep neural networks are becoming a de-facto standard. Nowadays, computing facilities based on the Von Neumann architecture are devoted to these tasks, yet rapidly hitting a bottleneck in performance and energy efficiency. The in-memory computing (IMC) architecture emerged as a revolutionary approach to overcome that issue. In this work, we propose an IMC architecture based on resistive switching memory (RRAM) crossbar arrays to provide a convenient primitive for matrix-vector multiplication in a single computational step. This opens massive performance improvement in the acceleration of a neural network that is frequently used in survival analysis of biomedical records, namely the DeepSurv. We explored how the synaptic weights mapping strategy and the programming algorithms developed to counter RRAM non-idealities expose a performance/energy trade-off. Finally, we discussed how this application is tailored for the IMC architecture rather than being executed on commodity systems.

Keywords: drift; in-memory computing (IMC); multi level conductance; resistive RAM (RRAM); survival analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The handling editor FMP declared a past collaboration with the authors CZ, CW, PO, and DI.

Figures

Figure 1
Figure 1
The structure of the DeepSurv neural network according to the implementation provided in Katzman et al. (2018). The dropout layers between inputs and hidden layers are not shown for clarity.
Figure 2
Figure 2
(A) Crossbar array architecture for matrix-vector-multiplication (MVM) operations. (B) Schematic of a 1T1R resistive switching memory (RRAM) device integrated into the 4 kbits array used in this work. (C) I–V characteristics of a 1T1R RRAM device measured for increasing VG proving multi-level conductance (MLC) capability. (D) The RIFLE test equipment used in this work.
Figure 3
Figure 3
(A) Algorithms used in RRAM forming, set, and reset operation modes. The voltages during the operation and the verify phases are evidenced. (B) Global flowchart scheme, representing the different steps for ML-SET and ML-Hybrid algorithms.
Figure 4
Figure 4
(A) L2-L9 levels distribution in RRAM obtained after the application of the programming algorithm. (B) L2-L9 levels distribution in RRAM after 168 h evidencing the drift. (C) Evolution in time of the L5 distribution for ML-Set algorithm. (D) Same study performed for the ML-Hybrid algorithm.
Figure 5
Figure 5
(A) An example of the application of the incremental network quantization (INQ). algorithm. (B) cumulative distribution function (CDF) of the C-index retrieved in Monte Carlo simulations with different weight picking strategies compared with the C-index obtained by a graphic processing unit (GPU) without quantization in training and working with full floating-point precision.
Figure 6
Figure 6
(A) Colormap of the conductance σ of the differential distribution obtained through ML-Set at the end of the programming algorithm. (B) and after 168 h evidencing the effect of the drift. (C,D) Same analysis performed for ML-Hybrid. The lower is better for DeepSurv accuracy.
Figure 7
Figure 7
RRAM-based implementation of the DeepSurv neural network considering the 64 × 64 crossbars studied in this work. The additional circuitry, such as ADCs, DACs, and DSPs, required for the operations outside the MVMs are highlighted as well.
Figure 8
Figure 8
(A) Quantization error rate colormap of the differential distribution obtained through ML-Set at the end of the programming algorithm. (B) After 168 h evidencing the effect of the drift. (C,D) The same analysis performed for ML-Hybrid. The lower is better for DeepSurv accuracy.
Figure 9
Figure 9
Histogram of the weight distribution.
Figure 10
Figure 10
(A) Boxplot of the C-Index value over 1,000 simulation with the distribution obtained from ML-Set at the end of the programming algorithm. (B) Boxplot of the C-Index value over 1,000 simulation with the distribution obtained from ML-Set after 168 h evidencing the effect of the drift. (C,D) The same analysis performed for ML-Hybrid.
Figure 11
Figure 11
Power consumption for MVM operation as a function of the conductance level selected as starting point for differential weight computation.
Figure 12
Figure 12
Benchmark of proposed RRAM-based IMC architecture and algorithms in terms of (A) energy consumption for each inference and (B) energy efficiency.
See this image and copyright information in PMC

References

    1. Allegra A., Tonacci A., Sciaccotta R., Genovese S., Musolino C., Pioggia G., et al. . (2022). Machine learning and deep learning applications in multiple myeloma diagnosis, prognosis, and treatment selection. Cancers 14, 1–16. 10.3390/cancers14030606 - DOI - PMC - PubMed
    1. Ambrogio S., Balatti S., Cubeta A., Calderoni A., Ramaswamy N., Ielmini D. (2014a). Statistical fluctuations in HfOx resistive-switching memory: part i - set/reset variability. IEEE Trans. Electron. Devices 61, 2912–2919. 10.1109/TED.2014.2330200 - DOI
    1. Ambrogio S., Balatti S., Cubeta A., Calderoni A., Ramaswamy N., Ielmini D. (2014b). Statistical fluctuations in HfOx resistive-switching memory: part II–random telegraph noise. IEEE Trans. Electron. Devices 61, 2920–2927. 10.1109/TED.2014.2330202 - DOI
    1. Ambrogio S., Balatti S., McCaffrey V., Wang D. C., Ielmini D. (2015a). Noise-induced resistance broadening in resistive switching memory–part i: intrinsic cell behavior. IEEE Trans. Electron. Devices 62, 3805–3811. 10.1109/TED.2015.2475598 - DOI
    1. Ambrogio S., Balatti S., McCaffrey V., Wang D. C., Ielmini D. (2015b). Noise-induced resistance broadening in resistive switching memory–part ii: array statistics. IEEE Trans. Electron. Devices 62, 3812–3819. 10.1109/TED.2015.2477135 - DOI

LinkOut - more resources