On the evolutionary language game in structured and adaptive populations
- PMID: 36040912
- PMCID: PMC9426894
- DOI: 10.1371/journal.pone.0273608
On the evolutionary language game in structured and adaptive populations
Abstract
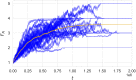
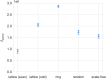
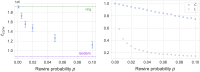
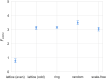
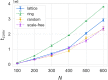
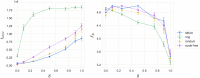
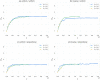
We propose an evolutionary model for the emergence of shared linguistic convention in a population of agents whose social structure is modelled by complex networks. Through agent-based simulations, we show a process of convergence towards a common language, and explore how the topology of the underlying networks affects its dynamics. We find that small-world effects act to speed up convergence, but observe no effect of topology on the communicative efficiency of common languages. We further explore differences in agent learning, discriminating between scenarios in which new agents learn from their parents (vertical transmission) versus scenarios in which they learn from their neighbors (oblique transmission), finding that vertical transmission results in faster convergence and generally higher communicability. Optimal languages can be formed when parental learning is dominant, but a small amount of neighbor learning is included. As a last point, we illustrate an exclusion effect leading to core-periphery networks in an adaptive networks setting when agents attempt to reconnect towards better communicators in the population.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



Similar articles
-
Culture and biology in the origins of linguistic structure.Psychon Bull Rev. 2017 Feb;24(1):118-137. doi: 10.3758/s13423-016-1166-7. Psychon Bull Rev. 2017. PMID: 28120320 Free PMC article.
-
How to reach linguistic consensus: a proof of convergence for the naming game.J Theor Biol. 2006 Oct 21;242(4):818-31. doi: 10.1016/j.jtbi.2006.05.024. Epub 2006 Jun 7. J Theor Biol. 2006. PMID: 16843499
-
Chaos and language.Proc Biol Sci. 2004 Apr 7;271(1540):701-4. doi: 10.1098/rspb.2003.2643. Proc Biol Sci. 2004. PMID: 15209103 Free PMC article.
-
Language evolution in the laboratory.Trends Cogn Sci. 2010 Sep;14(9):411-7. doi: 10.1016/j.tics.2010.06.006. Epub 2010 Aug 2. Trends Cogn Sci. 2010. PMID: 20675183 Review.
-
Unity and disunity in evolutionary sciences: process-based analogies open common research avenues for biology and linguistics.Biol Direct. 2016 Aug 20;11:39. doi: 10.1186/s13062-016-0145-2. Biol Direct. 2016. PMID: 27544206 Free PMC article. Review.
Cited by
-
Accelerating language emergence by functional pressures.PLoS One. 2023 Dec 14;18(12):e0295748. doi: 10.1371/journal.pone.0295748. eCollection 2023. PLoS One. 2023. PMID: 38096195 Free PMC article.
References
-
- Fitch WT. The Evolution of Language. Cambridge: Cambridge University Press; 2010.
-
- Steels L. The Synthetic Modeling of Language Origins. Evolution of Communication. 1997;1(1):1–34. doi: 10.1075/eoc.1.1.02ste - DOI
-
- Kretzschmar J. Language and Complex Systems. Cambridge: Cambridge University Press; 2015.
-
- Dediu D, de Boer B. Language Evolution Needs Its Own Journal. Journal of Language Evolution. 2016;1(1):1–6. doi: 10.1093/jole/lzv001 - DOI
-
- Patriarca M, Heinsalu E, Leonard JL. Languages in Space and Time: Models and Methods from Complex Systems Theory. 1st ed. Cambridge University Press; 2020.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

