A Hybrid Scattering Transform for Signals with Isolated Singularities
- PMID: 36051382
- PMCID: PMC9425109
- DOI: 10.1109/ieeeconf53345.2021.9723364
A Hybrid Scattering Transform for Signals with Isolated Singularities
Abstract
The scattering transform is a wavelet-based model of Convolutional Neural Networks originally introduced by S. Mallat. Mallat's analysis shows that this network has desirable stability and invariance guarantees and therefore helps explain the observation that the filters learned by early layers of a Convolutional Neural Network typically resemble wavelets. Our aim is to understand what sort of filters should be used in the later layers of the network. Towards this end, we propose a two-layer hybrid scattering transform. In our first layer, we convolve the input signal with a wavelet filter transform to promote sparsity, and, in the second layer, we convolve with a Gabor filter to leverage the sparsity created by the first layer. We show that these measurements characterize information about signals with isolated singularities. We also show that the Gabor measurements used in the second layer can be used to synthesize sparse signals such as those produced by the first layer.
Keywords: deep learning; scattering transforms; sparsity; time-frequency analysis; wavelets.
Figures
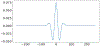
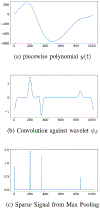
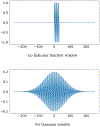

References
-
- Bekir Ahmad and Golomb Solomon W.. There are no further counterexamples to s. piccard’s theorem. IEEE Transactions on Information Theory, 53(8):2864–2867, 2007.
-
- Mallat Stéphane. A Wavelet Tour of Signal Processing, Third Edition: The Sparse Way. Academic Press, 3rd edition, 2008.
-
- Mallat Stéphane. Group invariant scattering. Communications on Pure and Applied Mathematics, 65(10):1331–1398, October 2012.
-
- Mallat Stéphane and Waldspurger Iréne. Phase retrieval for the cauchy wavelet transform. Journal of Fourier Analysis and Applications, 21(6):1251–1309, 2015.
-
- Ranieri Juri, Chebira Amina, Lu Yue M., and Vetterli Martin. Phase retrieval for sparse signals: Uniqueness conditions. CoRR, abs/1308.3058, 2013.
Grants and funding
LinkOut - more resources
Full Text Sources
