Viscoelastic properties of suspended cells measured with shear flow deformation cytometry
- PMID: 36053000
- PMCID: PMC9576269
- DOI: 10.7554/eLife.78823
Viscoelastic properties of suspended cells measured with shear flow deformation cytometry
Abstract
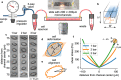
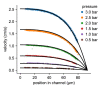
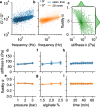
Numerous cell functions are accompanied by phenotypic changes in viscoelastic properties, and measuring them can help elucidate higher level cellular functions in health and disease. We present a high-throughput, simple and low-cost microfluidic method for quantitatively measuring the elastic (storage) and viscous (loss) modulus of individual cells. Cells are suspended in a high-viscosity fluid and are pumped with high pressure through a 5.8 cm long and 200 µm wide microfluidic channel. The fluid shear stress induces large, ear ellipsoidal cell deformations. In addition, the flow profile in the channel causes the cells to rotate in a tank-treading manner. From the cell deformation and tank treading frequency, we extract the frequency-dependent viscoelastic cell properties based on a theoretical framework developed by R. Roscoe [1] that describes the deformation of a viscoelastic sphere in a viscous fluid under steady laminar flow. We confirm the accuracy of the method using atomic force microscopy-calibrated polyacrylamide beads and cells. Our measurements demonstrate that suspended cells exhibit power-law, soft glassy rheological behavior that is cell-cycle-dependent and mediated by the physical interplay between the actin filament and intermediate filament networks.
Keywords: cell biology; cell rheology; human; microfluidics; mouse; shear flow; tank treading; viscoelasticity.
Plain language summary
Cells in the human body are viscoelastic: they have some of the properties of an elastic solid, like rubber, as well as properties of a viscous fluid, like oil. To carry out mechanical tasks – such as, migrating through tissues to heal a wound or to fight inflammation – cells need the right balance of viscosity and elasticity. Measuring these two properties can therefore help researchers to understand important cell tasks and how they are impacted by disease. However, quantifying these viscous and elastic properties is tricky, as both depend on the time-scale they are measured: when pressed slowly, cells appear soft and liquid, but they turn hard and thick when rapidly pressed. Here, Gerum et al. have developed a new system for measuring the viscosity and elasticity of individual cells that is fast, simple, and inexpensive. In this new method, cells are suspended in a specialized solution with a consistency similar to machine oil which is then pushed with high pressure through channels less than half a millimeter wide. The resulting flow of fluid shears the cells, causing them to elongate and rotate, which is captured using a fast camera that takes 500 images per second. Gerum et al. then used artificial intelligence to extract each cell’s shape and rotation speed from these images, and calculated their viscosity and elasticity based on existing theories of how viscoelastic objects behave in fluids. Gerum et al. also investigated how the elasticity and viscosity of cells changed with higher rotation frequencies, which corresponds to shorter time-scales. This revealed that while higher frequencies made the cells appear more viscous and elastic, the ratio between these two properties remained the same. This means that researchers can compare results obtained from different experimental techniques, even if the measurements were carried out at completely different frequencies or time-scales. The method developed by Gerum et al. provides a fast an inexpensive way for analyzing the viscosity and elasticity of cells. It could also be a useful tool for screening the effects of drugs, or as a diagnostic tool to detect diseases that affect the mechanical properties of cells.
© 2022, Gerum et al.
Conflict of interest statement
RG is inventor in a patent application on this method (EP22150396.4) alongside SG and BF, EM, ME, JE, AM, AB, SS, AW, JB, LF, SA, RG, SG, JG, SS, NS, MN, HH, DS, FR, SM No competing interests declared, SG, BF is an inventor in a patent application on this method (EP22150396.4)
Figures
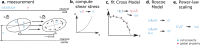







References
-
- Abadi M. Tensorflow: A system for large-scale machine learning. In 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI; 2016. pp. 265–283.
-
- Alcaraz J, Buscemi L, Puig-de-Morales M, Colchero J, Baró A, Navajas D. Correction of microrheological measurements of soft samples with atomic force microscopy for the hydrodynamic drag on the cantilever. Langmuir. 2002;18:716–721. doi: 10.1021/la0110850. - DOI
-
- Balland M, Desprat N, Icard D, Féréol S, Asnacios A, Browaeys J, Hénon S, Gallet F. Power laws in microrheology experiments on living cells: comparative analysis and modeling. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics. 2006;74:021911. doi: 10.1103/PhysRevE.74.021911. - DOI - PubMed
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

