A General Iterative Clustering Algorithm

Abstract

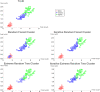
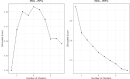
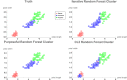
The quality of a cluster analysis of unlabeled units depends on the quality of the between units dissimilarity measures. Data dependent dissimilarity is more objective than data independent geometric measures such as Euclidean distance. As suggested by Breiman, many data driven approaches are based on decision tree ensembles, such as a random forest (RF), that produce a proximity matrix that can easily be transformed into a dissimilarity matrix. A RF can be obtained using labels that distinguish units with real data from units with synthetic data. The resulting dissimilarity matrix is input to a clustering program and units are assigned labels corresponding to cluster membership. We introduce a General Iterative Cluster (GIC) algorithm that improves the proximity matrix and clusters of the base RF. The cluster labels are used to grow a new RF yielding an updated proximity matrix which is entered into the clustering program. The process is repeated until convergence. The same procedure can be used with many base procedures such as the Extremely Randomized Tree ensemble. We evaluate the performance of the GIC algorithm using benchmark and simulated data sets. The properties measured by the Silhouette Score are substantially superior to the base clustering algorithm. The GIC package has been released in R: https://cran.r-project.org/web/packages/GIC/index.html.

Keywords: Clustering; Extremely Randomized Tree; Extremely randomized tree; Proximity; Random Forest; iterative RF clustering.

FIGURE 1

Scatterplots of petal length versus petal width features for the iris data for ground truth and 4 clustering methods. Ground truth clusters are setosa, versicolor and virginica shown in the upper left plot

FIGURE 2

Scatterplots of maximum heart rate achieved versus exercise‐induced ST depression for the heart disease data, for ground truth and 4 clustering methods

FIGURE 3

Silhouette scores over the range possible cluster numbers for the iris data. Note that the range of the ordinates in the two plots are not the same. The maximum for RFC is 6 and for IRFC is 2

FIGURE 4

Scatterplots of petal length versus petal width for the iris data for the number of clusters that maximized the Silhouette scores, 6 for RFC and 2 for IRFC. Ground truth with 3 clusters are shown in the upper left plot in Figure 1

FIGURE 5

Scatterplots of petal length versus petal width for the iris data for different initial labeling strategies all assuming 3 clusters. Ground truth clusters are shown in the upper left