Ultrafast Force-Clamp Spectroscopy of Microtubule-Binding Proteins
- PMID: 36063336
- PMCID: PMC9662813
- DOI: 10.1007/978-1-0716-2229-2_22
Ultrafast Force-Clamp Spectroscopy of Microtubule-Binding Proteins
Abstract
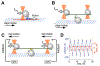
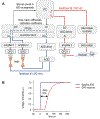
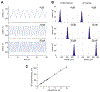
Optical trapping has been instrumental for deciphering translocation mechanisms of the force-generating cytoskeletal proteins. However, studies of the dynamic interactions between microtubules (MTs) and MT-associated proteins (MAPs) with no motor activity are lagging. Investigating the motility of MAPs that can diffuse along MT walls is a particular challenge for optical-trapping assays because thermally driven motions rely on weak and highly transient interactions. Three-bead, ultrafast force-clamp (UFFC) spectroscopy has the potential to resolve static and diffusive translocations of different MAPs with sub-millisecond temporal resolution and sub-nanometer spatial precision. In this report, we present detailed procedures for implementing UFFC, including setup of the optical instrument and feedback control, immobilization and functionalization of pedestal beads, and preparation of MT dumbbells. Example results for strong static interactions were generated using the Kinesin-7 motor CENP-E in the presence of AMP-PNP. Time resolution for MAP-MT interactions in the UFFC assay is limited by the MT dumbbell relaxation time, which is significantly longer than reported for analogous experiments using actin filaments. UFFC, however, provides a unique opportunity for quantitative studies on MAPs that glide along MTs under a dragging force, as illustrated using the kinetochore-associated Ska complex.
Keywords: Bead functionalization; CENP-E kinesin; Kinetochore; Microtubule-associated proteins; Microtubule-dependent diffusion; Molecular friction; Ska complex; Ultrafast force-clamp spectroscopy.
© 2022. The Author(s), under exclusive license to Springer Science+Business Media, LLC, part of Springer Nature.
Figures

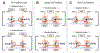







References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

