Dilatational and shear rheology of soluble and insoluble monolayers with a Langmuir trough
- PMID: 36063630
- PMCID: PMC10038177
- DOI: 10.1016/j.jcis.2022.08.051
Dilatational and shear rheology of soluble and insoluble monolayers with a Langmuir trough
Abstract
Hypothesis: The surface dilatational and shear moduli of surfactant and protein interfacial layers can be derived from surface pressures measured with a Wilhelmy plate parallel, ΔΠpar and perpendicular ΔΠperp to the barriers in a Langmuir trough.
Experimental: Applying area oscillations, A0+ ΔAeiωt, in a rectangular Langmuir trough induces changes in surface pressure, ΔΠpar and ΔΠperp for monolayers of soluble palmitoyl-lysophosphatidylcholine (LysoPC), insoluble dipalmitoylphosphatidylcholine (DPPC), and the protein β-lactoglobulin to evaluate Es∗+Gs∗=A0ΔΠparΔA and Es∗-Gs∗=A0ΔΠperpΔA. Gs∗ was independently measured with a double-wall ring apparatus (DWR) and Es∗ by area oscillations of hemispherical bubbles in a capillary pressure microtensiometer (CPM) and the results were compared to the trough measurements.
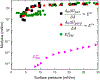
Findings: For LysoPC and DPPC, A0ΔΠparΔA≅A0ΔΠperpΔA meaning Es∗≫Gs∗ and Es∗≅A0ΔΠparΔA≅A0ΔΠperpΔA. Trough values for Es∗ were quantitatively similar to CPM when corrected for interfacial curvature. DWR showed G∗ was 4 orders of magnitude smaller than Es∗ for both LysoPC and DPPC. For β-lactoglobulin films, A0ΔΠparΔA>A0ΔΠperpΔA and Es∗ and Gs∗ were in qualitative agreement with independent CPM and DWR measurements. For β-lactoglobulin, both Es∗ and Gs∗ varied with film age and history on the trough, suggesting the evolution of the protein structure.
Keywords: DPPC; Dilatational modulus; Interfacial dilatational rheology; Interfacial rheology; Interfacial shear rheology; Lysolipids; Phospholipids; Soluble surfactant; β-lactoglobulin.
Copyright © 2022 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures

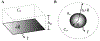
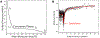

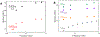
Similar articles
-
A miniaturized radial Langmuir trough for simultaneous dilatational deformation and interfacial microscopy.J Colloid Interface Sci. 2021 Jan 15;582(Pt B):1085-1098. doi: 10.1016/j.jcis.2020.08.053. Epub 2020 Aug 25. J Colloid Interface Sci. 2021. PMID: 32932179
-
Insoluble layer deposition and dilatational rheology at a microscale spherical cap interface.Soft Matter. 2016 Aug 17;12(33):7038-55. doi: 10.1039/c5sm03133h. Soft Matter. 2016. PMID: 27478885
-
Self-assembly of monoglycerides in beta-lactoglobulin adsorbed films at the air-water interface. Structural, topographical, and rheological consequences.Biomacromolecules. 2006 Sep;7(9):2661-70. doi: 10.1021/bm060144r. Biomacromolecules. 2006. PMID: 16961330
-
Separating viscoelastic and compressibility contributions in pressure-area isotherm measurements.Adv Colloid Interface Sci. 2014 Apr;206:428-36. doi: 10.1016/j.cis.2013.09.005. Epub 2013 Sep 29. Adv Colloid Interface Sci. 2014. PMID: 24103106 Review.
-
Dynamic interfacial properties of human tear-lipid films and their interactions with model-tear proteins in vitro.Adv Colloid Interface Sci. 2016 Jul;233:4-24. doi: 10.1016/j.cis.2015.12.009. Epub 2015 Dec 23. Adv Colloid Interface Sci. 2016. PMID: 26830077 Review.
Cited by
-
Exploring the Use of a Lipopeptide in Dipalmitoylphosphatidylcholine Monolayers for Enhanced Detection of Glyphosate in Aqueous Environments.Langmuir. 2024 Jul 2;40(26):13583-13595. doi: 10.1021/acs.langmuir.4c01089. Epub 2024 Jun 22. Langmuir. 2024. PMID: 38907731 Free PMC article.
-
Influence of Cholesterol on the Insertion and Interaction of SARS-CoV-2 Proteins with Lipid Membranes.ACS Appl Bio Mater. 2025 Jun 16;8(6):5380-5394. doi: 10.1021/acsabm.5c00776. Epub 2025 Jun 6. ACS Appl Bio Mater. 2025. PMID: 40474679 Free PMC article.
-
Evolution of interfacial mechanics of lung surfactant mimics progression of acute respiratory distress syndrome.Proc Natl Acad Sci U S A. 2023 Dec 19;120(51):e2309900120. doi: 10.1073/pnas.2309900120. Epub 2023 Dec 12. Proc Natl Acad Sci U S A. 2023. PMID: 38085774 Free PMC article.
-
Curvature- and temperature-dependent transport of soluble surfactant mixtures to the air-aqueous surface with applications in fluorine-free firefighting foams.J Colloid Interface Sci. 2025 Jul 15;690:137082. doi: 10.1016/j.jcis.2025.02.090. Epub 2025 Feb 15. J Colloid Interface Sci. 2025. PMID: 40138923
-
New experiments and models to describe soluble surfactant adsorption above and below the critical micelle concentration.J Colloid Interface Sci. 2025 Jan;677(Pt A):557-568. doi: 10.1016/j.jcis.2024.07.204. Epub 2024 Jul 27. J Colloid Interface Sci. 2025. PMID: 39111091
References
-
- Cicuta P, Terentjev EM, Viscoelasticity of a protein monolayer from anisotropic surface pressure measurements. Eur. Phys. J. E 16, 147–158 (2005). - PubMed
-
- Kanthe AD, Krause M, Zheng S, Ilott A, Bu W, Bera MK, Lin B, Maldarelli C, Tu RS, Armoring the interface with surfactants to prevent the adsorption of monoclonal antibodies. ACS Applied Mater Interfaces, (2020). - PubMed
-
- Alvarez NJ, Walker LM, Anna SL, Diffusion-limited adsorption to a spherical geometry: the impact of curvature and competitive time scales. Phys Rev E Stat Nonlin Soft Matter Phys 82, 011604 (2010). - PubMed
-
- Kotula AP, Anna SL, Insoluble layer deposition and dilatational rheology at a microscale spherical cap interface. Soft Matter 12, 7038–7055 (2016). - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

