Design Solutions for Slender Bars with Variable Cross-Sections to Increase the Critical Buckling Force

Abstract

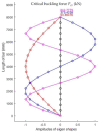
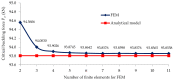
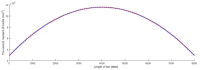
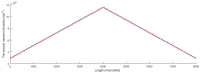
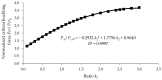
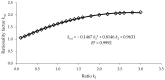
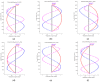
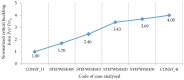
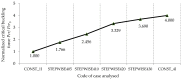
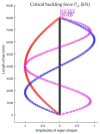
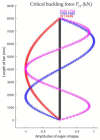
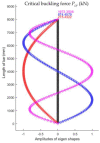
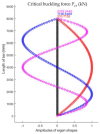
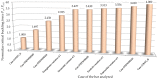
In large metal civil constructions (stadium roofs, bridges), slender bars can lose their stability under compression loading. There is a lack in the literature regarding design solutions and methods for increasing the critical buckling force of bars with variable cross-sections. The aim of this research is to present a numerical model with finite elements used for a comparative analysis of increasing the critical force of stability loss in cases of (i) bars with stepwise variation in the cross-sections and (ii) bars with continuous variation in the moment of inertia along the bar axis (parabolic, sinusoidal, triangular, and trapezoidal variation). Considering the large-scale applications in civil engineering, bars that were pin-connected at one end and simple-supported at the other end were analyzed. Firstly, the analytical model was described to compute the critical buckling force for bars with stepwise variation in the cross-sections. Then, a finite element model for a slender bar and the assumptions considered were presented. The results were computed using the MATLAB program based on the numerical model proposed and were validated with the analytical model for stepwise variable cross-sections of the bars. The numerical model was adapted for bars with continuous variation in the moment of inertia along the bar axis. It was shown that, by trapezoidal variation in the second moment of inertia along the axis of a bar, i.e., as buckling occurred in the elastic field, the critical buckling force could be increased by 3.556 times compared to a bar with a constant section. It was shown that there was certain bar with stepwise variation in the cross-section for which the critical buckling force was approximately equal to the one obtained for the bar with sinusoidal variation in the moment of inertia (increased by 3.427 times compared to a bar with a constant section).

Keywords: buckling; civil engineering; columns; numerical analysis; slender bars; stability; variable cross-section.

Figure 1

Bar analyzed having a stepwise variable cross-section whose bottom end is pin-connected, while the upper end is simply supported: (a) geometrical model of the entire bar and deformed shape at stability loss; (b) geometrical model considering the symmetry condition; (c) bending-moment diagram.

Figure 2

Characteristics of the finite elements of the bar double-embedded at both ends in terms of both the internal forces and flections (displacement and rotation) developed at the nodes.

Figure 3

The first three shapes of stability loss and corresponding critical buckling forces for the bar, whose geometrical and material characteristics are given in Table 1.

Figure 4

Analysis concerning the convergence of the solution obtained for the critical buckling load by the FEM compared with respect to the value computed with the analytical model.

Figure 5

Parabolic variation in the second moment of inertia I along the bar axis.

Figure 6

Geometrical model for a bar with parabolic variation in the second moment of inertia along the bar axis: (a) isometric view and (b) longitudinal section.

Figure 7

Sinusoidal variation in the second moment of inertia along the bar axis.

Figure 8

Geometrical model for s bar with sinusoidal variation in the second moment of inertia along the bar axis: (a) isometric view and (b) longitudinal section.

Figure 9

Triangular variation in the second moment of inertia along the bar axis.

Figure 10

Geometrical model for a bar with triangular variation in the second moment of inertia along the bar axis: (a) isometric view and (b) longitudinal section.

Figure 11

Trapezoidal variation in the second moment of inertia along the bar axis.

Figure 12

Geometrical model for a bar with trapezoidal variation in the second moment of inertia along the bar axis: (a) isometric view and (b) longitudinal section.

Figure 13

Variation in the normalized critical buckling force $P_{cr}/P_{cr0}$. computed with Equation (25) considering $k_1=4$ related to the ratio $k_2$.

Figure 14

Variation in the rationality factor $k_{rat}$. computed with Equation (37) considering $k_1=4$. related to the ratio $k_2$.

Figure 15

The first three shapes of stability loss and corresponding critical forces $P_{cr}$. obtained by the FEM for the six cases of bars analyzed: (a) CONST_1I; (b) STEPWISE405; (c) STEPWISE410; (d) STEPWISE420; (e) STEPWISE430; and (f) CONST_4I (details about each case are given in Table 2).

Figure 16

Comparison of the normalized critical buckling forces $P_{cr}/P_{cr0}$. computed with the finite element models for the bars involved (details about each case are given in Table 2).

Figure 17

Comparison of the normalized critical buckling forces $P_{cr}/P_{cr0}$ computed with the analytical model for the bars involved in this research (details about each case are given in Table 2).

Figure 18

The first three shapes of stability loss and corresponding critical buckling forces for the bar with parabolic variation in the second moment of inertia along the bar axis.

Figure 19

The first three shapes of stability loss and corresponding critical buckling forces for the bar with sinusoidal variation in the second moment of inertia along the bar axis.

Figure 20

The first three eigenshapes of stability loss and corresponding values for the critical buckling forces for the bar with triangular variation in the second moment of inertia along the bar axis.

Figure 21

The first three shapes of stability loss and corresponding values for the critical buckling force for the bar with trapezoidal variation in the second moment of inertia along the bar axis.

Figure 22

Comparison of the critical buckling force obtained by the FEM for all the cases of bars involved in this research.