SCATTERING STATISTICS OF GENERALIZED SPATIAL POISSON POINT PROCESSES

Abstract

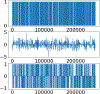
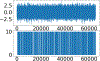
We present a machine learning model for the analysis of randomly generated discrete signals, modeled as the points of an inhomogeneous, compound Poisson point process. Like the wavelet scattering transform introduced by Mallat, our construction is naturally invariant to translations and reflections, but it decouples the roles of scale and frequency, replacing wavelets with Gabor-type measurements. We show that, with suitable nonlinearities, our measurements distinguish Poisson point processes from common self-similar processes, and separate different types of Poisson point processes.

Keywords: Poisson point process; Scattering transform; convolutional neural network.

Fig. 1.

First-order invariant scattering moments of homogeneous compound Poisson point processes with the same intensity λ₀ and different A_i. Left: Realizations of the process with arrival rates given by Top: A_i = 1 Middle: A_i are normal random variables Bottom: A_i are Rademacher random variables. Middle: Plots of normalized first-order scattering $\frac{SY(s,\xi ,1)}{s\Vert w{\Vert }_1}$ moments with p = 1.Right: Plots of normalized first-order scattering $\frac{SY(s,\xi ,2)}{s\Vert w{\Vert }_2^2}$ moments with p = 2.

Fig. 1.

First-order invariant scattering moments of homogeneous compound Poisson point processes with the same intensity λ₀ and different A_i. Left: Realizations of the process with arrival rates given by Top: A_i = 1 Middle: A_i are normal random variables Bottom: A_i are Rademacher random variables. Middle: Plots of normalized first-order scattering $\frac{SY(s,\xi ,1)}{s\Vert w{\Vert }_1}$ moments with p = 1.Right: Plots of normalized first-order scattering $\frac{SY(s,\xi ,2)}{s\Vert w{\Vert }_2^2}$ moments with p = 2.

Fig. 1.

First-order invariant scattering moments of homogeneous compound Poisson point processes with the same intensity λ₀ and different A_i. Left: Realizations of the process with arrival rates given by Top: A_i = 1 Middle: A_i are normal random variables Bottom: A_i are Rademacher random variables. Middle: Plots of normalized first-order scattering $\frac{SY(s,\xi ,1)}{s\Vert w{\Vert }_1}$ moments with p = 1.Right: Plots of normalized first-order scattering $\frac{SY(s,\xi ,2)}{s\Vert w{\Vert }_2^2}$ moments with p = 2.

Fig. 2.

First-order scattering moments for inhomogeneous Poisson point processes. Left: Sample realization with $\lambda (t)=0.01\left(1+0.5\sin \left(\frac{2\pi t}{N}\right)\right)$. Right: Time-dependent scattering moments $\frac{S_{\gamma ,p}Y(t)}{s\Vert w{\Vert }_P^p}$ at $t_1=\frac{N}{4}$, $t_2=\frac{N}{2}$,$t_3=\frac{3N}{4}$. Note that the scattering coefficients at times t₁, t₂, t₃ converges to λ(t₁) = 0.015, λ(t₂) = 0.01, λ(t₃) = 0.005.

Fig. 2.

First-order scattering moments for inhomogeneous Poisson point processes. Left: Sample realization with $\lambda (t)=0.01\left(1+0.5\sin \left(\frac{2\pi t}{N}\right)\right)$. Right: Time-dependent scattering moments $\frac{S_{\gamma ,p}Y(t)}{s\Vert w{\Vert }_P^p}$ at $t_1=\frac{N}{4}$, $t_2=\frac{N}{2}$,$t_3=\frac{3N}{4}$. Note that the scattering coefficients at times t₁, t₂, t₃ converges to λ(t₁) = 0.015, λ(t₂) = 0.01, λ(t₃) = 0.005.

Fig. 3.

First-order invariant scattering moments for standard Brownian motion and Poisson point process. Left: Sample realizations Top: Brownian motion. Bottom: Ordinary Poisson point process. Middle: Normalized scattering moments $\frac{S{Y}_{\text{poisson}}(x,\xi ,p)}{\lambda \mathbb{E}{\left|A_1\right|}^p\Vert w{\Vert }_p^p}$ and $\frac{S{X}_{\text{BM}}(s,\xi ,p)}{\lambda \mathbb{E}|Z{|}^p\Vert w{\Vert }_p^p}$ for Poisson and BM with p = 1. Right: The same but with p = 2.

Fig. 3.

First-order invariant scattering moments for standard Brownian motion and Poisson point process. Left: Sample realizations Top: Brownian motion. Bottom: Ordinary Poisson point process. Middle: Normalized scattering moments $\frac{S{Y}_{\text{poisson}}(x,\xi ,p)}{\lambda \mathbb{E}{\left|A_1\right|}^p\Vert w{\Vert }_p^p}$ and $\frac{S{X}_{\text{BM}}(s,\xi ,p)}{\lambda \mathbb{E}|Z{|}^p\Vert w{\Vert }_p^p}$ for Poisson and BM with p = 1. Right: The same but with p = 2.

Fig. 3.

First-order invariant scattering moments for standard Brownian motion and Poisson point process. Left: Sample realizations Top: Brownian motion. Bottom: Ordinary Poisson point process. Middle: Normalized scattering moments $\frac{S{Y}_{\text{poisson}}(x,\xi ,p)}{\lambda \mathbb{E}{\left|A_1\right|}^p\Vert w{\Vert }_p^p}$ and $\frac{S{X}_{\text{BM}}(s,\xi ,p)}{\lambda \mathbb{E}|Z{|}^p\Vert w{\Vert }_p^p}$ for Poisson and BM with p = 1. Right: The same but with p = 2.