DEVELOPMENT OF FIBRIN BRANCH STRUCTURE BEFORE AND AFTER GELATION
- PMID: 36093310
- PMCID: PMC9455619
- DOI: 10.1137/21m1401024
DEVELOPMENT OF FIBRIN BRANCH STRUCTURE BEFORE AND AFTER GELATION
Abstract
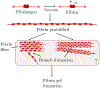
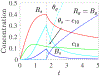
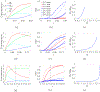
In [Fogelson and Keener, Phys. Rev. E, 81 (2010), 051922], we introduced a kinetic model of fibrin polymerization during blood clotting that captured salient experimental observations about how the gel branching structure depends on the conditions under which the polymerization occurs. Our analysis there used a moment-based approach that is valid only before the finite time blow-up that indicates formation of a gel. Here, we extend our analyses of the model to include both pre-gel and post-gel dynamics using the PDE-based framework we introduced in [Fogelson and Keener, SIAM J. Appl. Math., 75 (2015), pp. 1346-1368]. We also extend the model to include spatial heterogeneity and spatial transport processes. Studies of the behavior of the model reveal different spatial-temporal dynamics as the time scales of the key processes of branch formation, monomer introduction, and diffusion are varied.
Keywords: 82C26; 82D60; 92C05; 92C45; blood clotting; fibrin branching; gel front; generating function; kinetic gelation; polymer diffusion.
Figures





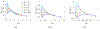




References
-
- Blombäck B, Carlsson K, Fatah K, Hessel B, and Procyk R, Fibrin in human plasma: Gel architectures governed by rate and nature of fibrinogen activation, Thromb Res, 75 (1994), pp. 521–538. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
