On the impermanence of species: The collapse of genetic incompatibilities in hybridizing populations

Abstract

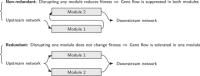
Species pairs often become genetically incompatible during divergence, which is an important source of reproductive isolation. An idealized picture is often painted where incompatibility alleles accumulate and fix between diverging species. However, recent studies have shown both that incompatibilities can collapse with ongoing hybridization, and that incompatibility loci can be polymorphic within species. This paper suggests some general rules for the behavior of incompatibilities under hybridization. In particular, we argue that redundancy of genetic pathways can strongly affect the dynamics of intrinsic incompatibilities. Since fitness in genetically redundant systems is unaffected by introducing a few foreign alleles, higher redundancy decreases the stability of incompatibilities during hybridization, but also increases tolerance of incompatibility polymorphism within species. We use simulations and theories to show that this principle leads to two types of collapse: in redundant systems, exemplified by classical Dobzhansky-Muller incompatibilities, collapse is continuous and approaches a quasi-neutral polymorphism between broadly sympatric species, often as a result of isolation-by-distance. In nonredundant systems, exemplified by co-evolution among genetic elements, incompatibilities are often stable, but can collapse abruptly with spatial traveling waves. As both types are common, the proposed principle may be useful in understanding the abundance of genetic incompatibilities in natural populations.

Keywords: Genetic redundancy; hybridization; incompatibility; purging of incompatibilities; reproductive isolation.

Figure 1

Synopsis of the duality between genetic redundancy and the stability of incompatibilities to hybridization. A “module” refers to a set of factors in a genetic/biochemical network (Schlosser & Wagner, 2004), often associated with an input–output relationship (e.g., a regulatory pathway of downstream genes).

Figure 2

Schematic differences between the collapse dynamics of redundant and non‐redundant incompatibilities. For simplicity, species 1 is subject to unidirectional gene flow from species 2. (A) Representation of dynamics in the general model. Red lines depict the trajectories of genotype distributions in species 1 subject to unidirectional gene flow from species 2. Contours depict the fitness landscape in the genotype distribution space $\mathsf{G}$. For redundant incompatibilities, collapse trajectories form a quasi‐neutral path on the fitness plateau. For nonredundant incompatibilities, collapse requires a stochastic jump. (B) Explicit examples of dynamics in two‐locus models (see Section “Specific models”. Nonredundant: Model I; Redundant: Model II).

Figure 3

The collapse of two locus incompatibilities in a population subject to gene flow from a different species. Blue trajectories are frequencies of the native haplotype in the focal population (AB for Model I, and Ab for Model II). The trajectories show results of 50 repeated simulations of the birth–death process. Simulations have the following recombination probabilities: $r=0.055$ for Model I, and $r=0.25$ for Model II. Recombination probabilities were chosen such that population size in the range ${10}^3\le N\le {10}^4$ has a non‐negligible impact on collapse dynamics. Numerically calculated mean collapse times $⟨t_c⟩$ using Equations (12) and (11) are shown as heatmaps. All data in this figure correspond to fixed parameters: $s=10,\alpha =1,m=0.01$.

Figure 4

Nonredundant incompatibility collapses via traveling waves in spatial systems. (A) The coarse‐grained system of Model I between sympatric species. Once the initial state is broken by a local collapse, the collapsed deme has to survive swamping. If it escapes swamping, the rate of flipping is higher towards the exterior of the collapsed region, which drives the propagation of traveling waves. Gray (+1) and white (‐1) boxes correspond to two coarse‐grained states of a single deme. m and $m^{\prime }$ are hybridization and migration probabilities, respectively. (B) Two examples of SLiM simulations of Model I showing that symmetric incompatibilities could collapse completely or form multiple tension zones. Frequencies of allele A were taken every five generations (i.e., $\mathrm{\Delta }t=5$ in Equation 13). Hybridization probability $m=0.05$, and nearest‐neighbor migration probability $m^{\prime }=0.1$. Population size in each deme fluctuates around 539 for the iteration where total collapse occurs (top panels), and it fluctuates around 269 where multiple collapses occur (bottom panels). See Supporting Information Figure S3 for the behaviors of all loci. (C) Numerical solutions of conditional transition probabilities among the four states of the entire system. Parameters are the same as SLiM simulations with population sizes fixed at 269. Probabilities are derived from transition rates by inversing ${⟨t_c⟩}_{\mathrm{non}}$ from Equation S26.

Figure 5

SLiM simulations demonstrate how redundant incompatibilities collapse into quasi‐neutral polymorphisms in broadly sympatric species. Heatmaps are frequencies of allele A across space and time taken every five generations (i.e., $\mathrm{\Delta }t=5$ in Equation 13). For all three models, hybridization probability is $m=0.05$, and nearest‐neighbor migration probability is $m^{\prime }=0.1$. Population size in each deme fluctuates around 269. In deviation from neutrality, red lines are expectations under neutral genetic drift. See Figure S4 for the behaviors of all loci.

Figure 6

The collapse of redundant incompatibilities are limited by dispersal outside regions of sympatry. (A) Schematics of the collapse outside regions of sympatry. Gray color represents frequencies of a hypothetical incompatibility allele. These frequencies form a spatial continuum determined by the dispersal process. Since frequencies are smooth, no discrete states are distinguishable (compare to nonredundant incompatibilities in Figure 4a) (B) SLiM simulations of Models II, III, and IV under a population structure where the zone of sympatric overlap has five consecutive demes, and there are 250 demes forming a one‐dimensional array outside the region of sympatry in each species. Each model was run for 100 realizations, and allele frequencies (p, blue curves) were taken at generation $t=9901$. The region of sympatry has five consecutive demes, and there are 250 demes forming a one‐dimensional array outside this region in each species. Hybridization probability $m=0.05$, and nearest‐neighbor migration probability $m^{\prime }=0.1$. Solid red lines are the probability $p_s$ calculated using Equation (14) with ${\sigma }^2=m^{\prime }$. Dashed red lines are the ensemble‐average $⟨p⟩$ of allele frequencies p. See Figure S5 for the behaviors of all loci.