Connecting the free energy principle with quantum cognition

Abstract

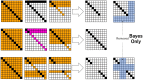
It appears that the free energy minimization principle conflicts with quantum cognition since the former adheres to a restricted view based on experience while the latter allows deviations from such a restricted view. While free energy minimization, which incorporates Bayesian inference, leads to a Boolean lattice of propositions (classical logic), quantum cognition, which seems to be very dissimilar to Bayesian inference, leads to an orthomodular lattice of propositions (quantum logic). Thus, we address this challenging issue to bridge and connect the free energy minimization principle with the theory of quantum cognition. In this work, we introduce "excess Bayesian inference" and show that this excess Bayesian inference entails an underlying orthomodular lattice, while classic Bayesian inference entails a Boolean lattice. Excess Bayesian inference is implemented by extending the key idea of Bayesian inference beyond classic Bayesian inference and its variations. It is constructed by enhancing the idea of active inference and/or embodied intelligence. The appropriate lattice structure of its logic is obtained from a binary relation transformed from a distribution of the joint probabilities of data and hypotheses by employing a rough-set lattice technique in accordance with quantum cognition logic.

Keywords: Bayesian inference; free energy minimization; lattice theory; quantum cognition; rough set.

Figure 1

A diagonal relation and its corresponding lattice, which is a Boolean lattice. The lattice is shown here as a Hasse diagram, in which the elements of the lattice (a subset of D) are represented by black circles, and if one element is smaller than another element (i.e., one set is included in the other) and no element exists between them, then they are connected by a line, and the larger one is shown above the smaller one.

Figure 2

Snapshots of the joint probability between data and hypotheses. The probabilities are colored from low to high in the order of white, pale yellow, orange, pink, and black. By following the thick arrow, the binary relation R is obtained. The pale blue cells represent the domain in the relation, which is ignored by Bayesian inference.

Figure 3

Snapshots of the joint probabilities of data and hypotheses and their corresponding relation R. The articulation of the data and hypotheses with respect to the diagonal elements is determined by Equation 22. The joint probabilities are colored from low to high in the order of white, pale yellow, orange, pink, and black. The last diagram in the sequence ordered by the arrows represents a binary relation. A black cell at (h, d) represents (h, d)∈R, and a white cell represents (h, d)∉R.

Figure 4

Snapshots of the joint probabilities of data and hypotheses and their corresponding relation R. The articulation of the data and hypotheses with respect to the diagonal elements is determined by Equation 23. The joint probabilities are colored from low to high in the order of white, pale yellow, orange, pink, and black (left). A black cell at (h, d) represents (h, d)∈R, and a white cell represents (h, d)∉R (center right).

Figure 5

Relation between data and hypotheses consisting of (2 × 2), (3 × 3), (9 × 9), (6 × 6) diagonal relations and their corresponding Boolean lattices. All relations outside the diagonal relations constitute the greatest element, which fuses all the other Boolean lattices.

Figure 6

Disjoint union of some Boolean lattices, the least and greatest elements of which are common to all Boolean lattices. This is obtained from the relation shown in Figure 5.