External drivers of BOLD signal's non-stationarity

Abstract

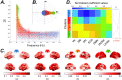
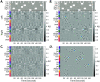
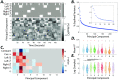
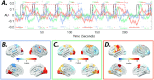
A fundamental challenge in neuroscience is to uncover the principles governing how the brain interacts with the external environment. However, assumptions about external stimuli fundamentally constrain current computational models. We show in silico that unknown external stimulation can produce error in the estimated linear time-invariant dynamical system. To address these limitations, we propose an approach to retrieve the external (unknown) input parameters and demonstrate that the estimated system parameters during external input quiescence uncover spatiotemporal profiles of external inputs over external stimulation periods more accurately. Finally, we unveil the expected (and unexpected) sensory and task-related extra-cortical input profiles using functional magnetic resonance imaging data acquired from 96 subjects (Human Connectome Project) during the resting-state and task scans. This dynamical systems model of the brain offers information on the structure and dimensionality of the BOLD signal's external drivers and shines a light on the likely external sources contributing to the BOLD signal's non-stationarity. Our findings show the role of exogenous inputs in the BOLD dynamics and highlight the importance of accounting for external inputs to unravel the brain's time-varying functional dynamics.

Fig 1. Synthetic LTI system with unknown inputs.

(A) A schematic of the brain as a network, where the nodes represent brain regions, and the edges represent connections between regions. The activity of four observed regions is modeled as a four-dimensional LTI system, and the influence of the unobserved regions and external stimuli into each node as an unknown driver. The synthetic system matrix is designed with eigenmodes oscillating at 0.01 and 0.06 Hz to mimic the frequencies of BOLD signal’s neurophysiological component. (B) Simulated time-evolution of each node’s activity (sampling rate = 1.4 Hz) is color-coded and shown in the presence of drivers, namely the internal noise and the external input (brighter colors). Only the blue node receives external input indicated by the magenta line. Three periods (I–III) are highlighted dashed lines. At period I (3–6 min), there is no external stimulation. At period II (9–12 min), the blue node is stimulated in 25 samples = 18 seconds blocks, interleaved with similarly sized rest periods. At period III (15–18 min), the blue node is stimulated for 7 samples = 5.04 seconds, with inter-stimulus intervals of 3 samples = 2.16 seconds. (C) Left panels show the estimated inputs to the blue node (green line, arbitrary units AU) estimated from a single simulation. The panels on the right show the average input and its standard error over 100 simulations. (D) The average 2-norm and standard error of the difference between the system’s true and estimated matrices of a 3-minute sliding window. (E) The color-coded lines show the average (and standard error) loading of each node on input matrix B.

Fig 2. Extracting spatiotemporal profiles of unknown external drivers in simulated brain dynamics.

(A &D) Estimated external inputs (i.e., B×U) to all brain regions from synthetic time series generated from a sample subject’s internal system parameters and (B & E) the average estimated external inputs across all subjects (input matrix B dimension = 7, regularization factor = 0.5). Brain regions (y-axis) are sorted based on resting-state networks identified by [50], namely the visual (Vis), sensory/motor (SM), dorsal attention (DN), ventral attention/salience (VN/Sal), limbic, executive control (ECN), and default mode network (DMN). System parameters in panels D & E are estimated from the stimulation window, however system parameters in panels A & B are estimated from same-length windows without external inputs. (C) Ground-truth synthetic inputs over 1000 samples (TR = 0.72 sec). (F) The similarity between ground-truth and estimated inputs. The system matrix A estimated from windows without external stimulation results in a significantly higher correlation between the vectorized estimated external and ground-truth input matrices (t−test, p < 0.05, p = 6.6 × 10⁻⁶⁵ and p = 2.9 × 10⁻⁶⁶ for estimation windows with 1000 and 250 samples, respectively), compared to system matrix A estimated from the stimulation windows (indicated by ‘*’ markers). The smaller estimation windows significantly (t−test, p < 0.05, p = 1.15 × 10⁻⁴⁵) reduce the estimated and ground-truth inputs’ similarity, only for the system matrix A estimated over stimulation windows (indicated by ‘*’ markers). The correlation values between the ground-truth and group average estimated inputs are indicated by ‘o’ markers.

Fig 3. Eigenmodes estimated from the full (1200 TR ≈14.5 min) resting-state time series.

(A) Distribution of frequency versus stability of eigenvalues during resting-state. Clustering the eigenvalues based on their eigenvector’s similarity highlights the spectral profile of different systems. All eigenvectors from all subjects were normalized and grouped into 4 clusters using the k-means clustering algorithm. We color-coded the clusters identified across subjects and all resting-state sessions (n = 4). (B) the inset plot shows the eigenvalues’ distribution. (C) The brain overlays represent the spatial distribution of the eigenvector associated with an eigenvalue (displayed with the same color code) that is at the centroid of each cluster.(D) The similarity between eigenvector clusters’ centroids and the resting-state networks. We performed spatial multiple linear regression analyses using all resting-state networks identified by [50], namely the visual (Vis), sensory/motor (SM), dorsal attention (DN), ventral attention/salience (VN/Sal), limbic, executive control (ECN), and default mode network (DMN) as the explanatory variables, to show which resting-state networks overlap with the eigenvector clusters’ centroids shown in the panel. The color-coded matrix shows the estimated normalized (divided by maximum value at each row) coefficients of the regression, calculated separately for every eigenvectors’ cluster’s centroid. The plot on the right shows the p-value and R² calculated for each cluster centroid.

Fig 4. Matching the spectral profile of the known and estimated external inputs.

(A–F) The difference between the average Fourier transform of the estimated inputs to all brain regions during tasks compared to that of other task conditions (see Materials and Methods for details). Top panels display the average (two sessions) spectral profile of the known boxcar regressors for each task (see S5 Fig in S1 File). Note the significant changes in the spectrum at expected task-specific frequency peaks across several brain regions, at low (<0.1 Hz) and high (>0.1 Hz) frequencies represented with red and green arrows, respectively. Frequencies for which brain regions did not pass the significance level (Wilcoxon rank-sum test, FDR p < 0.0005) are represented in black.

Fig 5. Average estimated external inputs in the motor task.

Internal system parameters (i.e., A matrices) during full-length resting-state and motor scans were used to estimate the external inputs in panels A & C, respectively. Panels B & D show time points form panels A & C with significantly higher or lower average inputs estimated during motor task than resting-state scans (paired t−test, p < 0.05, false discovery rate (FDR) corrected for multiple comparisons). Top plots in panels A & B show onsets and durations of visual cues and motor task conditions—left foot, left hand, right foot, right hand, and tongue movement blocks.

Fig 6. Principal component analysis of estimated external inputs.

(A) Group-level principal components (PCs) 1–15 calculated from concatenated estimated inputs (input matrix B dimension = 25) across all subjects. Top plots show onsets and durations of visual cues and motor task conditions. (B) Percent variance explained by PCs. Insets depict the percent variance explained by PCs 1–25. (C) t-values calculated from coefficients of multiple linear regression models of estimated external inputs associated with each PC (see methods for details). The average coefficients that fail to pass the significance-level across subjects (t−test, p < 0.05, Bonferroni corrected for multiple comparisons) are depicted in gray. (D) Distributions of R² values of multiple linear regression models in panel B for components with significant coefficients. White circles and color-coded horizontal bars indicate the medians and means of distributions, respectively. Pairwise comparison (Wilcoxon rank-sum test, p < 0.05, FDR corrected for multiple comparisons) between distributions reveal that R² values for principal components marked by red ‘*’ are significantly higher than those marked by black ‘o’ (except for the non-significant difference between PC 1 and PC 9). (E) Distributions of the number of lags (samples) that results in best fit (i.e., maximum R²) for PCs 1–9. We used the mean (round to nearest integer) of optimal subject-level lags for analysis in panels C and D.

Fig 7. Temporal and spatial profiles of estimated external inputs associated with visual cues.

(A) Color-coded lines show the mean and standard error (shaded area) of estimated inputs with the highest subject-level loadings for PCs 1 (green), 3 (orange), and 5 (blue). Time points with significant (t−test, p < 0.05, FDR corrected for multiple comparisons across time points) divergence from zero are marked with color-coded dots. The black and dashed red lines show the visual cue and motor task blocks, respectively. Color-coded panels (B-D) show the t−test values of brain regions with significant (t−test, p < 0.05, FDR corrected for multiple comparisons across ROIs) loadings on input matrix B rows corresponding to the aforementioned PCs.

Fig 8. Non-stationarity of estimated external inputs over resting-state scans.

(A) Brain overlays on top panels highlight regions with significantly (t − test, p < 0.05, FDR corrected for multiple comparisons) high normalized (z-scored over all brain regions) fluctuations (i.e., standard deviation) in the normalized (z-score) estimated inputs’ means, measured using sliding windows (6, 24, and 50 samples window length, TR = 0.72 sec). (B) Brain overlays on top panels highlight regions with significantly (t − test, p < 0.05, FDR corrected for multiple comparisons) high normalized (z-scored over all brain regions) nonlinear non-stationarity index developed by [49], calculated from the normalized (z-score) estimated inputs. The color-coded regions in the bottom plots in panels A and B highlight the allegiance of brain regions in top panels to the seven resting-state networks identified by [50].