Limits of epidemic prediction using SIR models
- PMID: 36125562
- PMCID: PMC9487859
- DOI: 10.1007/s00285-022-01804-5
Limits of epidemic prediction using SIR models
Abstract
The Susceptible-Infectious-Recovered (SIR) equations and their extensions comprise a commonly utilized set of models for understanding and predicting the course of an epidemic. In practice, it is of substantial interest to estimate the model parameters based on noisy observations early in the outbreak, well before the epidemic reaches its peak. This allows prediction of the subsequent course of the epidemic and design of appropriate interventions. However, accurately inferring SIR model parameters in such scenarios is problematic. This article provides novel, theoretical insight on this issue of practical identifiability of the SIR model. Our theory provides new understanding of the inferential limits of routinely used epidemic models and provides a valuable addition to current simulate-and-check methods. We illustrate some practical implications through application to a real-world epidemic data set.
Keywords: Epidemic prediction; Hypothesis testing; Identifiability; Nonlinear dynamics; Parameter inference; SIR model.
© 2022. The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature.
Conflict of interest statement
The authors declare no competing interests.
Figures



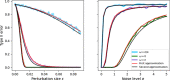
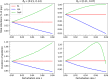





Similar articles
-
Modelling the spread of two successive SIR epidemics on a configuration model network.J Math Biol. 2025 Apr 23;90(5):51. doi: 10.1007/s00285-025-02207-y. J Math Biol. 2025. PMID: 40266328 Free PMC article.
-
Chaos analysis and explicit series solutions to the seasonally forced SIR epidemic model.J Math Biol. 2019 Jun;78(7):2235-2258. doi: 10.1007/s00285-019-01342-7. Epub 2019 Feb 26. J Math Biol. 2019. PMID: 30809691
-
Assessing inference of the basic reproduction number in an SIR model incorporating a growth-scaling parameter.Stat Med. 2018 Dec 20;37(29):4490-4506. doi: 10.1002/sim.7935. Epub 2018 Aug 16. Stat Med. 2018. PMID: 30117184
-
Mathematical models to characterize early epidemic growth: A review.Phys Life Rev. 2016 Sep;18:66-97. doi: 10.1016/j.plrev.2016.07.005. Epub 2016 Jul 11. Phys Life Rev. 2016. PMID: 27451336 Free PMC article. Review.
-
A Scoping Review of Drug Epidemic Models.Int J Environ Res Public Health. 2022 Feb 11;19(4):2017. doi: 10.3390/ijerph19042017. Int J Environ Res Public Health. 2022. PMID: 35206206 Free PMC article.
Cited by
-
Harnessing artificial intelligence for enhanced public health surveillance: a narrative review.Front Public Health. 2025 Jul 30;13:1601151. doi: 10.3389/fpubh.2025.1601151. eCollection 2025. Front Public Health. 2025. PMID: 40809756 Free PMC article. Review.
-
The disutility of compartmental model forecasts during the COVID-19 pandemic.Front Epidemiol. 2024 Jun 20;4:1389617. doi: 10.3389/fepid.2024.1389617. eCollection 2024. Front Epidemiol. 2024. PMID: 38966521 Free PMC article.
-
Quantum-Like Approaches Unveil the Intrinsic Limits of Predictability in Compartmental Models.Entropy (Basel). 2024 Oct 21;26(10):888. doi: 10.3390/e26100888. Entropy (Basel). 2024. PMID: 39451964 Free PMC article.
-
Assessing bias in susceptible-infected-recovered estimation from aggregated epidemic data.R Soc Open Sci. 2025 Jul 23;12(7):240526. doi: 10.1098/rsos.240526. eCollection 2025 Jul. R Soc Open Sci. 2025. PMID: 40708661 Free PMC article.
-
Accurately summarizing an outbreak using epidemiological models takes time.R Soc Open Sci. 2023 Sep 27;10(9):230634. doi: 10.1098/rsos.230634. eCollection 2023 Sep. R Soc Open Sci. 2023. PMID: 37771961 Free PMC article.
References
-
- Kermack WO, Mckendrick AG. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character. 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. - DOI
-
- Ross L-CSR. An application of the theory of probabilities to the study of a priori pathometry.-Part I. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character. 1916;92(638):204–230. doi: 10.1098/rspa.1916.0007. - DOI
-
- Ross L-CSR, Hudson HP. An application of the theory of probabilities to the study of a priori pathometry.-Part III. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character. 1917;93(650):225–240. doi: 10.1098/rspa.1917.0015. - DOI
-
- Ross R, Hudson HP. An application of the theory of probabilities to the study of a priori pathometry.-Part II. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character. 1917;93(650):212–225. doi: 10.1098/rspa.1917.0014. - DOI
-
- Brauer F, Castillo-Chavez C, Feng Z. Mathematical models in epidemiology. Texts in applied mathematics. New York, NY: Springer; 2019.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

