Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Sep 2;24(9):1238.
doi: 10.3390/e24091238.

Decoding 'Maximum Entropy' Deconvolution

Long V Le  1 , Tae Jung Kim  2 , Young Dong Kim  2 , David E Aspnes  3
Affiliations

Decoding 'Maximum Entropy' Deconvolution

Long V Le et al. Entropy (Basel). .

Abstract

For over five decades, the mathematical procedure termed "maximum entropy" (M-E) has been used to deconvolve structure in spectra, optical and otherwise, although quantitative measures of performance remain unknown. Here, we examine this procedure analytically for the lowest two orders for a Lorentzian feature, obtaining expressions for the amount of sharpening and identifying how spurious structures appear. Illustrative examples are provided. These results enhance the utility of this widely used deconvolution approach to spectral analysis.

Keywords: deconvolution; maximum entropy; spectral analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Comparison of Lorentzian, pseudo-Lorentzian, and B/A lineshapes.
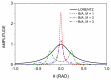
Figure 2
Figure 2
B/A processing of the single Lorentzian (bottom spectrum) for M = 1, 2, and 3. All lineshapes are to scale.
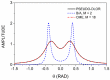
Figure 3
Figure 3
Result of B/A processing of a double-peaked model spectrum. Details are given in the text.
Figure 4
Figure 4
Results of B/A and CME processing of a double-peaked model spectrum. Details are given in the text.
See this image and copyright information in PMC

References

    1. Burg J.P. Maximum Entropy Spectral Analysis. Stanford University; Stanford, CA, USA: 1975. Stanford Exploration Project.
    1. Ulrych T. Maximum Entropy Power Spectrum of Long Period Geomagnetic Reversals. Nature. 1972;235:218–219. doi: 10.1038/235218a0. - DOI
    1. Willingale R. Use of the maximum entropy method in X-ray astronomy. Mon. Not. R. Astron. Soc. 1981;194:359–364. doi: 10.1093/mnras/194.2.359. - DOI
    1. Narayan R., Nityananda R. Maximum Entropy Image Restoration in Astronomy. Annu. Rev. Astron. Astrophys. 1986;24:127–170. doi: 10.1146/annurev.aa.24.090186.001015. - DOI
    1. Wells J.W., Birkinshaw K. A matrix approach to resolution enhancement of XPS spectra by a modified maximum entropy method. J. Electron Spectrosc. Relat. Phenom. 2006;152:37–43. doi: 10.1016/j.elspec.2006.03.003. - DOI

LinkOut - more resources