Multiclass Classification of Metrologically Resourceful Tripartite Quantum States with Deep Neural Networks

Abstract

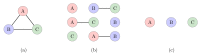
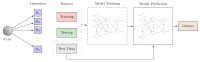
Quantum entanglement is a unique phenomenon of quantum mechanics, which has no classical counterpart and gives quantum systems their advantage in computing, communication, sensing, and metrology. In quantum sensing and metrology, utilizing an entangled probe state enhances the achievable precision more than its classical counterpart. Noise in the probe state preparation step can cause the system to output unentangled states, which might not be resourceful. Hence, an effective method for the detection and classification of tripartite entanglement is required at that step. However, current mathematical methods cannot robustly classify multiclass entanglement in tripartite quantum systems, especially in the case of mixed states. In this paper, we explore the utility of artificial neural networks for classifying the entanglement of tripartite quantum states into fully separable, biseparable, and fully entangled states. We employed Bell's inequality for the dataset of tripartite quantum states and train the deep neural network for multiclass classification. This entanglement classification method is computationally efficient due to using a small number of measurements. At the same time, it also maintains generalization by covering a large Hilbert space of tripartite quantum states.

Keywords: Heisenberg limit; artificial neural networks; deep neural networks; multiclass classification; quantum entanglement; quantum metrology; quantum sensing.

Figure 1

Tripartite entanglement classes depicting (a) fully entangled, (b) biseparable, and (c) fully separable systems.

Figure 2

Different schemes depicting the use of quantum entanglement in quantum sensing and metrology experiments. Herein, the circle represents the probe state, the square represents the unitary evolution that encodes the unknown parameter $\eta$, the ellipse represents entangling operations, and the semicircle represents the measurement. (a) The quantum entanglement is only employed in the measurement, (b) the quantum entanglement is employed in the probe state, (c) both the probe state and measurement employ quantum entanglement, and (d) both the probe state and measurement employ quantum entanglement and the ancillary system is also included with entanglement.

Figure 3

Stages in quantum sensing and metrology with an additional step for detection and classification of resourceful states.

Figure 4

An ANN model for training, testing, and prediction.

Figure 5

A DNN model with three hidden layers ($n_{\mathrm{d}}=3$) for classification of tripartite states. Green nodes represent input units where the number $n_{\mathrm{f}}$ of features is equal to 4 for Mermin and 8 for Svetlichny inequality. Blue nodes represent the hidden nodes where the ReLu is chosen as the activation function. Red nodes represent the output units where Softmax is used as the activation function.

Figure 6

Classification accuracy as a function of the number of hidden neurons, $n_{\mathrm{h}}$ in a single hidden layer ($n_{\mathrm{d}}=1$) for Mermin ($n_{\mathrm{f}}=4$) and Svetlichny ($n_{\mathrm{f}}=8$) features. No hidden neuron ($n_{\mathrm{h}}=0$) corresponds to linear optimization with no hidden layer.

Figure 7

Training/validation (a) accuracy and (b) loss of the $\mathrm{Bell}-\mathrm{DNN}\left(8,3,80\right)$ classifier as a function of the number of epochs for Svetlichny features.

Figure 8

Classification accuracy of the $\mathrm{Bell}-\mathrm{DNN}\left(8,n_{\mathrm{d}},n_{\mathrm{h}}\right)$ model as a function of the number of hidden neurons, $n_{\mathrm{h}}$ for Svetlichny features when $n_{\mathrm{d}}=1,2,3,4$.