Relative binding free energy calculations with transformato: A molecular dynamics engine-independent tool

Abstract

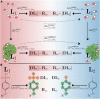
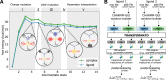
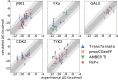
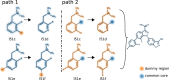
We present the software package transformato for the setup of large-scale relative binding free energy calculations. Transformato is written in Python as an open source project (https://github.com/wiederm/transformato); in contrast to comparable tools, it is not closely tied to a particular molecular dynamics engine to carry out the underlying simulations. Instead of alchemically transforming a ligand L ₁ directly into another L ₂, the two ligands are mutated to a common core. Thus, while dummy atoms are required at intermediate states, in particular at the common core state, none are present at the physical endstates. To validate the method, we calculated 76 relative binding free energy differences $\Delta \Delta G_{L_1\to L_2}^{bind}$ for five protein-ligand systems. The overall root mean squared error to experimental binding free energies is 1.17 kcal/mol with a Pearson correlation coefficient of 0.73. For selected cases, we checked that the relative binding free energy differences between pairs of ligands do not depend on the choice of the intermediate common core structure. Additionally, we report results with and without hydrogen mass reweighting. The code currently supports OpenMM, CHARMM, and CHARMM/OpenMM directly. Since the program logic to choose and construct alchemical transformation paths is separated from the generation of input and topology/parameter files, extending transformato to support additional molecular dynamics engines is straightforward.

Keywords: automated setup; binding affinity; free energy; molecular dynamics simulation; open source; python (programming language).

FIGURE 1

(A) Comparison of alchemical paths used in traditional setups (dotted, horizontal arrows) and in the CC/SAI approach (thick, horizontal arrows) implemented in transformato to compute relative binding free energy differences. Free energies are calculated relative to non-physical intermediate states, the common core [DL _i ]-R_CC (i = 1, 2), connecting the two ligands (L₁, L₂). Here [DL _i ] represents the atoms of each ligand not in the CC region and R_CC indicates the CC region itself. (B) The mutation path for calculating $\mathrm{\Delta }\mathrm{\Delta }{G}_{L_1\to L_2}^{bind}$ between a pair of ligands taken from the CDK2 dataset. The atoms that differ between the two ligands and, thus, are not present in the CC, are highlighted in color; these are transformed into dummy atoms (reddish circles). The common core is indicated by the green circles.

FIGURE 2

(A) Details of the mutation path from L ₁ shown in Figure 1B) to its CC to compute $\mathrm{\Delta }\mathrm{\Delta }{G}_{L_1\to [D{L}_1]-R_{CC}}^{\mathit{bind}}$ : (I) electrostatic interactions of the non-CC atoms are scaled to zero (three steps; step 1 in the diagram is the native, fully interacting ligand), (II) LJ interactions of the non-CC hydrogen atoms are turned off (one step), (III) LJ interactions of the three non-CC heavy atoms are turned off on an atom-by-atom basis (three steps), (IV) the last non-CC heavy atom is changed to the “junction” atom type X (one step), (V) the CC reached from L ₁ $(R_{c{c}_1})$ is adjusted to the one reached from L ₂ (cf. Figure 1B), in five steps. (B) Overview of the workflow when computing free energy differences with transformato.

FIGURE 3

ΔG ^bind calculated with transformato (blue triangles) compared to results obtained by pmx/CGenFF (for JNK1, GAL3, CDK2, TYK2) marked as orange crosses, by FEP+ (for JNK1, CDK2, TYK2) marked as red stars, and by AMBER (FXa) marked as green triangles. The respective RMSE and MAE values are listed in Table 2.

FIGURE 4

The two pathways for calculating ΔΔG ^bind (l51c → l51d) and ΔΔG ^bind (l51e → l51f) of the FXa dataset. Path 1: only a single hydrogen is mutated into a dummy atom (l51c, and l51e, l51f); then, as part of making the CC equivalent, the carbon it is bound to becomes a nitrogen atom (l51d and l51f). Path 2: the dummy region encompasses the compete aromatic ring plus the dimethylammoniomethyl group.

FIGURE 5

Results for selected mutations recomputed without HMR, using OpenMM, as well as CHARMM/OpenMM as the underlying MD engine. The reduced set consists of: GAL3, l4 → l3, l6 → l1; TYK2, jmc_28 → ejm_31, ejm_46 → ejm_31; FXa, l51a → l51d, l51c → l51bt; CDK2, 1h1s → 1h1q, 22 → 1h1q, 29 → 1h1q. (A) Plot of results calculated without HMR (timestep Δt = 1 fs, no constraints on the ligand and protein) against results with HMR (Δt = 4 fs, constraints on all bonds involving hydrogen atoms). For the selected mutations RMSE (ΔΔG ^bind ) = 0.30 kcal/mol, MAE (ΔΔG ^bind ) = 0.21 kcal/mol, Pearson’s R = 0.99, and Spearman’s ρ = 1.0. (B) Plot of the $\mathrm{\Delta }\mathrm{\Delta }{G}_{L_1\to L_2}^{bind}$ results for the mutations of the subset obtained with OpenMM with and without HMR, as well as CHARMM/OpenMM (no HMR). For the results without HMR, using OpenMM and CHARMM/OpenMM as the backend, respectively: RMSE (ΔΔG ^bind ) = 0.39 kcal/mol, MAE (ΔΔG ^bind ) = 0.35 kcal/mol, Pearson’s R = 0.98, and Spearman’s ρ = 1.0.