The inspection paradox: An important consideration in the evaluation of rotor lifetimes in cardiac fibrillation

Abstract

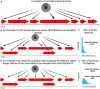
Background and Objective: Renewal theory is a statistical approach to model the formation and destruction of phase singularities (PS), which occur at the pivots of spiral waves. A common issue arising during observation of renewal processes is an inspection paradox, due to oversampling of longer events. The objective of this study was to characterise the effect of a potential inspection paradox on the perception of PS lifetimes in cardiac fibrillation. Methods: A multisystem, multi-modality study was performed, examining computational simulations (Aliev-Panfilov (APV) model, Courtmanche-Nattel model), experimentally acquired optical mapping Atrial and Ventricular Fibrillation (AF/VF) data, and clinically acquired human AF and VF. Distributions of all PS lifetimes across full epochs of AF, VF, or computational simulations, were compared with distributions formed from lifetimes of PS existing at 10,000 simulated commencement timepoints. Results: In all systems, an inspection paradox led towards oversampling of PS with longer lifetimes. In APV computational simulations there was a mean PS lifetime shift of +84.9% (95% CI, ± 0.3%) (p < 0.001 for observed vs overall), in Courtmanche-Nattel simulations of AF +692.9% (95% CI, ±57.7%) (p < 0.001), in optically mapped rat AF +374.6% (95% CI, $\pm$ 88.5%) (p = 0.052), in human AF mapped with basket catheters +129.2% (95% CI, ±4.1%) (p < 0.05), human AF-HD grid catheters 150.8% (95% CI, $\pm$ 9.0%) (p < 0.001), in optically mapped rat VF +171.3% (95% CI, ±15.6%) (p < 0.001), in human epicardial VF 153.5% (95% CI, ±15.7%) (p < 0.001). Conclusion: Visual inspection of phase movies has the potential to systematically oversample longer lasting PS, due to an inspection paradox. An inspection paradox is minimised by consideration of the overall distribution of PS lifetimes.

Keywords: atrial fibrilation; cardiac fibrillation; inspection paradox; phase singularity; renewal theory; ventricular fibrillation.

FIGURE 1

(A) An example of a simple renewal process in which event lasts for a period of time, before a new occurs. (B) An example of a PS renewal process, where at any given time either one event could be ongoing, multiple events can occur simultaneously or no events could be active. Each event is sampled equally and individually. (C) The probability distribution of event lifetimes for a simulated sequence of event lifetimes (PS), consistent with other renewal processes and our previous work. The mean PS lifetime is 112 ms. (D) An example where PS lifetimes are sampled according to the moment of observation, rather than properly examining the full distribution of lifetimes around it. Due to an inspection paradox, it is more likely for longer lasting events to be observed rather than short lasting ones. (E) To demonstrate how an inspection paradox can lead to a bias in favor of longer lasting events, 10,000 randomly chosen commencement timepoints where chosen, with the lifetimes of PS occurring at those timepoints sampled. The probability distribution demonstrates suggests that longer lasting events had a higher probability of occurring, compared with the overall distribution This is reflected in the mean lifetime of this distribution being 222 ms.

FIGURE 2

(A) The experimentally acquired data, clinically acquired data, and computational simulations utilized in this study. (B) Shows presents an example of PS detected and tracked on a phase map. (C) Demonstrates the distribution of PS lifetimes when all PS are properly sampled from an epoch of fibrillation. (D) Demonstrates the distribution of PS lifetimes when only PS present at a randomly chosen timepoint (such as the commencement of a recording) are observed.

FIGURE 3

(A–D) Presents an example case of an APV simulation. (B,G) presents the overall distribution of PS lifetimes across a full epoch of their respective model systems. (C,H) Demonstrate the distribution of observed PS sampled at the 10,000 commencement timepoints. (D,I) Presents the cumulative distribution functions (CDF) of the overall and observed PS lifetimes. (E) shows the boxplot of mean lifetime shifts across n = 10 APV cases, with an increase in the mean PS lifetime of +19.7 ms (95% CI, ± 0.1 ms) and an overall lifetime shift of +84.9% (95% CI, ± 0.3%). (p < 0.001 for observed vs. overall). (F–I) presents an example case of a 2D computational model of fibrillation. (J) For n = 4 cases, there was an increase in mean PS lifetimes of +45.5 (95% CI, ± 1.9 ms) and an overall lifetime shift of +692.9% (95% CI, ± 57.7%). (p < 0.001 for observed vs. overall).

FIGURE 4

The influence of an inspection paradox on AF data. (A–D) Presents an example case of optically mapped rat AF, (F–I) presents an example case of basket catheter recorded human AF, (K–N) Presents an example case of HD grid recorded human AF. (B,G,L) Presents the overall distribution of PS lifetimes across full epochs of AF. (C,H,M) Demonstrates the distribution of observed PS sampled at the 10,000 commencement timepoints. (D,I,M) Presents the cumulative distribution functions (CDF) of the overall and observed PS lifetimes. (E) In n = 3 cases of optical mapping, the increase in mean PS lifetime was 122.6 ms (95% CI, ± 27.5 ms) and the overall mean PS lifetime shift was +374.6% (95% CI, ± 88.5%) (p = 0.052 for observed vs. overall). (J) In n = 10 cases, the increase in mean PS lifetime was 78.8 ms (95% CI, ± 9.2 ms) and the overall mean lifetime shift of PS was +129.2% (95% CI, ± 4.1%) (p = 0.04 for observed vs. overall). (O) In n = 10 cases, the increase in mean PS lifetime was 64.3 ms (95% CI, ± 5.8 ms) and the overall mean PS lifetime shift was +150.8 (95% CI, ± 9.0%) (p < 0.001 for observed vs. overall).

FIGURE 5

The Influence of an inspection paradox on VF data. (A–D) Show an example case of optically mapped rat VF, and (F–I) shows an example case of human VF recording through a 256 electrode epicardial sock. (B,G) Show the overall distribution of PS lifetimes across full epochs of VF. (C,H) Show the distribution of PS lifetimes observed across the 10,000 samples. (D,I) Presents the cumulative distribution functions (CDF) of the overall and observed PS lifetimes. (E) In optically mapped rat VF, there was an increase in the mean PS lifetime of +40.0 ms (95% CI, ±5.1 ms) and an overall mean lifetime shift of +171.3% (95% CI, ± 15.6%) (p < 0.001 for observed vs. overall). (J) In human VF, in n = 8 cases, there was an increase in the mean PS lifetime of +159.5 ms (95% CI, ±15.2 ms) and an overall mean lifetime shift of +153.5% (95% CI, ± 15.7%) (p < 0.001 for observed vs. overall).