Effect of Movement on the Early Phase of an Epidemic
- PMID: 36149585
- PMCID: PMC9510491
- DOI: 10.1007/s11538-022-01077-5
Effect of Movement on the Early Phase of an Epidemic
Abstract
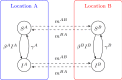
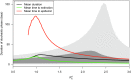
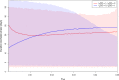
The early phase of an epidemic is characterized by a small number of infected individuals, implying that stochastic effects drive the dynamics of the disease. Mathematically, we define the stochastic phase as the time during which the number of infected individuals remains small and positive. A continuous-time Markov chain model of a simple two-patch epidemic is presented. An algorithm for formalizing what is meant by small is presented, and the effect of movement on the duration of the early stochastic phase of an epidemic is studied.
Keywords: Early spread of infection; Markov chain; Metapopulation.
© 2022. The Author(s), under exclusive licence to Society for Mathematical Biology.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures
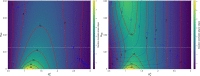

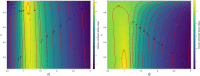



References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

