Geometry-informed irreversible perturbations for accelerated convergence of Langevin dynamics

Abstract

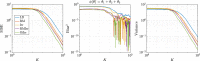
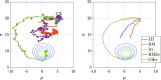
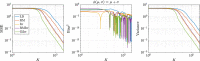
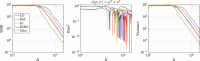
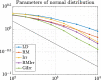
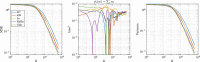
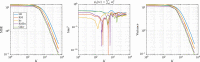
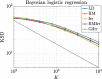
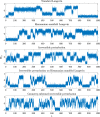
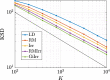
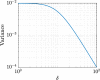
We introduce a novel geometry-informed irreversible perturbation that accelerates convergence of the Langevin algorithm for Bayesian computation. It is well documented that there exist perturbations to the Langevin dynamics that preserve its invariant measure while accelerating its convergence. Irreversible perturbations and reversible perturbations (such as Riemannian manifold Langevin dynamics (RMLD)) have separately been shown to improve the performance of Langevin samplers. We consider these two perturbations simultaneously by presenting a novel form of irreversible perturbation for RMLD that is informed by the underlying geometry. Through numerical examples, we show that this new irreversible perturbation can improve estimation performance over irreversible perturbations that do not take the geometry into account. Moreover we demonstrate that irreversible perturbations generally can be implemented in conjunction with the stochastic gradient version of the Langevin algorithm. Lastly, while continuous-time irreversible perturbations cannot impair the performance of a Langevin estimator, the situation can sometimes be more complicated when discretization is considered. To this end, we describe a discrete-time example in which irreversibility increases both the bias and variance of the resulting estimator.

Keywords: Bayesian computation; Geometry-informed irreversibility; Monte Carlo sampling; Riemannian manifold Langevin dynamics; Stochastic gradient Langevin dynamics.

Fig. 1

MSE of the running average for the first moment. Stochastic gradients are computed

Fig. 2

MSE of the running average for the second moment. Stochastic gradients are computed

Fig. 3

Kernelized Stein discrepancy plot for the Gaussian example. Black line has slope $-1/2$, which denotes the expected convergence rate

Fig. 4

Trajectory burn-in: each trajectory is run for $T=2.5$. Left: single trajectories, right: mean paths. The gradients are computed exactly here

Fig. 5

Observable: ${\varphi }_1(\mu ,\sigma )=\mu +\sigma$, $\delta =2$. Stochastic gradients are computed

Fig. 6

Observable: ${\varphi }_2(\mu ,\sigma )={\mu }^2+{\sigma }^2$, $\delta =2$. Stochastic gradients are computed

Fig. 7

Kernelized Stein discrepancy plot for the parameters of a normal distribution example. Black line has slope $-1/2$, which denotes the expected convergence rate

Fig. 8

Observable: ${\varphi }_1(w)={\sum }_i{w}_i$. Bayesian logistic regression. Here, $d=20$

Fig. 9

Observable: ${\varphi }_2(w)={\sum }_i{w}_i^2$. Bayesian logistic regression. Here, $d=20$

Fig. 10

Kernelized Stein discrepancy plot for Bayesian logistic regression example. Black line has slope $-1/2$, which denotes the expected convergence rate

Fig. 11

Posterior distribution sampled with standard Langevin with a deterministic gradient with $T=10000$ and $h={10}^{-4}$. Notice that the system is very multimodal and non-Gaussian

Fig. 12

Trace plots of the $W_{11}$ marginal

Fig. 13

Variance of running average estimators. For the second moment (middle plot), there is less difference among the samplers as the distribution is quite symmetric, and one can properly estimate the second moment even if the samplers are stuck in a single mode. GiIrr is able to estimate the observable with cross-moments (right plot) better than the other samplers

Fig. 14

Kernelized Stein discrepancy plot for the ICA example. Black line has slope $-1/2$, which denotes the expected convergence rate

Fig. 15

Variance for different $\delta$, fixed h

Fig. 16

(Squared) bias and variance of $\varphi (\theta )={\Vert \theta \Vert }^2$ for varying levels of irreversibility