Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia

Fedelis Mutiso¹, John L Pearce², Sara E Benjamin-Neelon^{3

4}, Noel T Mueller^{5

6}, Hong Li¹, Brian Neelon^{1

7}

Affiliations

¹ Division of Biostatistics, Department of Public Health Sciences, Medical University of South Carolina, Charleston, SC, USA.
² Division of Environmental Health, Department of Public Health Sciences, Medical University of South Carolina, Charleston, SC, USA.
³ Department of Health, Behavior and Society, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁴ Lerner Center for Public Health Promotion, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁵ Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁶ Welch Center for Prevention, Epidemiology and Clinical Research, Johns Hopkins University, Baltimore, MD, USA.
⁷ Charleston Health Equity and Rural Outreach Innovation Center (HEROIC), Ralph H. Johnson VA Health Care System, Charleston, SC, USA.

PMID: 36168515
PMCID: PMC9500097
DOI: 10.1016/j.spasta.2022.100703

Review

Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia

Fedelis Mutiso et al. Spat Stat. 2022 Dec.

. 2022 Dec:52:100703.

doi: 10.1016/j.spasta.2022.100703. Epub 2022 Sep 23.

Authors

Fedelis Mutiso¹, John L Pearce², Sara E Benjamin-Neelon^{3

4}, Noel T Mueller^{5

6}, Hong Li¹, Brian Neelon^{1

7}

Affiliations

¹ Division of Biostatistics, Department of Public Health Sciences, Medical University of South Carolina, Charleston, SC, USA.
² Division of Environmental Health, Department of Public Health Sciences, Medical University of South Carolina, Charleston, SC, USA.
³ Department of Health, Behavior and Society, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁴ Lerner Center for Public Health Promotion, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁵ Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA.
⁶ Welch Center for Prevention, Epidemiology and Clinical Research, Johns Hopkins University, Baltimore, MD, USA.
⁷ Charleston Health Equity and Rural Outreach Innovation Center (HEROIC), Ralph H. Johnson VA Health Care System, Charleston, SC, USA.

PMID: 36168515
PMCID: PMC9500097
DOI: 10.1016/j.spasta.2022.100703

Abstract

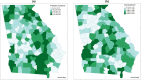
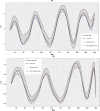
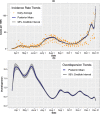
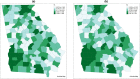
Overdispersed count data arise commonly in disease mapping and infectious disease studies. Typically, the level of overdispersion is assumed to be constant over time and space. In some applications, however, this assumption is violated, and in such cases, it is necessary to model the dispersion as a function of time and space in order to obtain valid inferences. Motivated by a study examining spatiotemporal patterns in COVID-19 incidence, we develop a Bayesian negative binomial model that accounts for heterogeneity in both the incidence rate and degree of overdispersion. To fully capture the heterogeneity in the data, we introduce region-level covariates, smooth temporal effects, and spatially correlated random effects in both the mean and dispersion components of the model. The random effects are assigned bivariate intrinsic conditionally autoregressive priors that promote spatial smoothing and permit the model components to borrow information, which is appealing when the mean and dispersion are spatially correlated. Through simulation studies, we show that ignoring heterogeneity in the dispersion can lead to biased and imprecise estimates. For estimation, we adopt a Bayesian approach that combines full-conditional Gibbs sampling and Metropolis-Hastings steps. We apply the model to a study of COVID-19 incidence in the state of Georgia, USA from March 15 to December 31, 2020.

Keywords: B -splines; Conditionally autoregressive prior; Overdispersion; Pólya-gamma distribution; Spatial data analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

**Fig. 1**
Descriptive maps for incidence rate and overdispersion from intercept–only models for data from March 15, 2020 to December 31, 2020 for the 159 counties in Georgia. Panel (a): Predicted incidence. Panel (b): Overdispersion. Legends correspond to sample quintiles.

**Fig. 2**
(a): Average time trend for the mean in simulation study. (b): Average time trend for dispersion in simulation study.

**Fig. 3**
Simulated and predicted random effects for the mean and dispersion components for Model 1: spatial NB model with correlated random intercepts. Panel (a): Simulated random intercept for the mean component. Panel (b): Predicted random intercept for the mean component. Panel (c): Simulated random intercept for dispersion component. Panel (d): Predicted random intercept for dispersion component. Legends correspond to sample quintiles.

**Fig. 4**
Daily incidence rate and overdispersion trends for the COVID-19 study. Panel (a): Mean incidence rate trend across counties. Panel (b): Mean overdispersion ( $α$ ) across counties.

**Fig. 5**
Model-based spatial random effect estimates for the COVID-19 study. Panel (a): Posterior mean predicted random effects for the mean component $(ϕ_{1})$ . Panel (b): Posterior mean predicted random effects for the dispersion component $(ϕ_{2})$ . Legends correspond to sample quintiles.

See this image and copyright information in PMC

References

1. Banerjee S., Carlin B., Gelfand A. second ed. CRC Press, Taylor and Francis Group; Boca Raton, FL: 2014. Hierarchical Modeling and Analysis for Spatial Data.
1. Best N.G., Ickstadt K., Wolpert R.L. Spatial Poisson regression for health and exposure data measured at disparate resolutions. J. Amer. Statist. Assoc. 2000;95(452):1076–1088. doi: 10.1080/01621459.2000.10474304. - DOI
1. Centers for Disease Control and Prevention N.G. 2018. Social vulnerability index 2018 database US. URL https://www.atsdr.cdc.gov/placeandhealth/svi/data_documentation_download....
1. Consul P. Marcel Dekker; New York, Basel: 1989. Generalized Poisson Distributions: Properties and Applications.
1. Eilers P.H.C., Marx B. Flexible smoothing with B-splines and penalties. Statist. Sci. 1996;11(2) doi: 10.1214/ss/1038425655. - DOI

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia

Affiliations

Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

References

Publication types

Grants and funding

LinkOut - more resources

Full Text Sources