Discrete element models for understanding the biomechanics of fossorial animals

Abstract

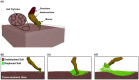
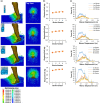
The morphological features of fossorial animals have continuously evolved in response to the demands of survival. However, existing methods for animal burrowing mechanics are not capable of addressing the large deformation of substrate. The discrete element method (DEM) is able to overcome this limitation. In this study, we used DEM to develop a general model to simulate the motion of an animal body part and its interaction with the substrate. The DEM also allowed us to easily change the forms of animal body parts to examine how those different forms affected the biomechanical functions. These capabilities of the DEM were presented through a case study of modeling the burrowing process of North American Badger. In the case study, the dynamics (forces, work, and soil displacements) of burrowing were predicted for different forms of badger claw and manus, using the model. Results showed that when extra digits are added to a manus, the work required for a badger to dig increases considerably, while the mass of soil dug only increases gradually. According to the proposed efficiency index (ratio of the amount of soil dug to the work required), the modern manus with 5 digits has indeed biomechanical advantage for their fossorial lifestyle, and the current claw curvature (25.3 mm in radius) is indeed optimal. The DEM is able to predict biomechanical relationships between functions and forms for any fossorial animals. Results can provide biomechanical evidences for explaining how the selective pressures for functions influence the morphological evolution in fossorial animals.

Keywords: badger; biomechanics; burrowing; discrete element method (DEM); soil.

FIGURE 1

A badger manus specimen provided by Beaty Biodiversity Museum (University of British Colombia, Vancouver, Canada).

FIGURE 2

Interaction model. (a) Substrate domain and a simplified animal body part (a spherical object) submerged in a substrate. (b) Velocity contour of substrate particles resulting from the object's motion. (c) Trajectory of the object in the substrate. (d) Substrate domain and the initial position of a simplified animal body part (a rectangular object). (e) Velocity contour of substrate resulting from the object's motion, showing the disturbance of substrate particles. (f) Soil resistance to the rectangular object over the distance of travel.

FIGURE 3

Examples of modeling various conditions of substrate. (a) Sand particles with a uniform diameter. (b) Cohesive soil with bonds between particles. (c) A stony soil. (d) Plant and tree materials on ground surface.

FIGURE 4

Badger manus and claw. (a) Example of a manus from a badger specimen and a 3D scan model. (b) Curvatures generated from the representative specimen of claw (Specimen No. 12, digit III). (c) Artificial claw models used for simulations.

FIGURE 5

Claw‐soil interaction model. (a) Soil domain and a claw before initiating soil cutting (t = 0 s); (b–d) The start of soil cutting (t = 0.03 s), the maximum depth of cutting (t = 0.06 s), and completion of cutting (t = 0.14 s), respectively

FIGURE 6

Badger manus models. (a) The 5‐digit manus from the 3D scan model of specimen No. 12. (b) 1‐, 2‐, 3‐, 4‐, 6‐, 7‐, and 8‐digit artificial manus in succession

FIGURE 7

Manus‐soil interaction model. (a) Soil domain, forelimb, and manus model before initiating soil digging (t = 0 s). (b–d) Start of soil digging (t = 0.18 s), maximum depth of digging (t = 0.28 s), completion of digging (t = 0.51 s) in a power stroke.

FIGURE 8

Results from the claw‐soil interaction model for different radii of curvature (R). (a) Cross‐sectional view of soil particle velocity contours resulting from the moving claw. (b) Top view of the amount of loosened soil at the completion of soil cutting. (c) Resistance forces experienced by claws in a soil cutting cycle. (d) Total mass of cut soil and maximum resistance force. (e) Relationship between R and the soil cutting depth (d). (f) Soil cutting efficiency, η _c (the ratio of the total mass of cut soil to the maximum resistance force).

FIGURE 9

Results from the manus‐soil interaction model for 1‐, 3‐, 5‐, and 8‐digit manus from the top to the bottom in succession. (a) Soil particle velocity contours from cross‐sectional and top views. (b) Accumulated mass of the displaced soil after each of four power strokes of digging. (c) Resistance force exerted on the manus during the four strokes of digging.

FIGURE 10

Work and digging efficiency. (a) Cumulative amount of work performed after every power stroke during soil digging by 1‐, 2‐, 3‐, 4‐, 5‐, 6‐, 7‐, and 8‐digit manus in succession. (b) Soil digging efficiency, η _d (the ratio of the total mass of displaced soil to the total work required for digging).