Inferring learning rules from animal decision-making
- PMID: 36177341
- PMCID: PMC9518972
Inferring learning rules from animal decision-making
Abstract
How do animals learn? This remains an elusive question in neuroscience. Whereas reinforcement learning often focuses on the design of algorithms that enable artificial agents to efficiently learn new tasks, here we develop a modeling framework to directly infer the empirical learning rules that animals use to acquire new behaviors. Our method efficiently infers the trial-to-trial changes in an animal's policy, and decomposes those changes into a learning component and a noise component. Specifically, this allows us to: (i) compare different learning rules and objective functions that an animal may be using to update its policy; (ii) estimate distinct learning rates for different parameters of an animal's policy; (iii) identify variations in learning across cohorts of animals; and (iv) uncover trial-to-trial changes that are not captured by normative learning rules. After validating our framework on simulated choice data, we applied our model to data from rats and mice learning perceptual decision-making tasks. We found that certain learning rules were far more capable of explaining trial-to-trial changes in an animal's policy. Whereas the average contribution of the conventional REINFORCE learning rule to the policy update for mice learning the International Brain Laboratory's task was just 30%, we found that adding baseline parameters allowed the learning rule to explain 92% of the animals' policy updates under our model. Intriguingly, the best-fitting learning rates and baseline values indicate that an animal's policy update, at each trial, does not occur in the direction that maximizes expected reward. Understanding how an animal transitions from chance-level to high-accuracy performance when learning a new task not only provides neuroscientists with insight into their animals, but also provides concrete examples of biological learning algorithms to the machine learning community.
Figures
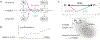
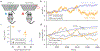
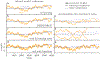
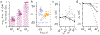

References
-
- Ashwood ZC, Roy NA, Stone IR, Laboratory TIB, Churchland AK, Pouget A, and Pillow JW. Mice alternate between discrete strategies during perceptual decision-making. bioRxiv, page 2020.10.19.346353, Oct. 2020. doi: 10.1101/2020.10.19.346353. URL https://www.biorxiv.org/content/10.1101/2020.10.19.346353v1. - DOI - DOI - PMC - PubMed
-
- Bak JH, Choi JY, Akrami A, Witten I, and Pillow JW. Adaptive optimal training of animal behavior. In Lee DD, Sugiyama M, Luxburg UV, Guyon I, and Garnett R, editors, Advances in Neural Information Processing Systems 29, pages 1947–1955, 2016.
-
- Bishop CM. Pattern recognition and machine learning. Springer, 2006.
Grants and funding
LinkOut - more resources
Full Text Sources
