From classical mendelian randomization to causal networks for systematic integration of multi-omics

Abstract

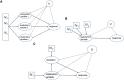
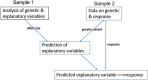
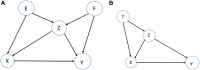
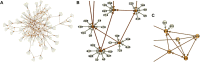
The number of studies with information at multiple biological levels of granularity, such as genomics, proteomics, and metabolomics, is increasing each year, and a biomedical questaion is how to systematically integrate these data to discover new biological mechanisms that have the potential to elucidate the processes of health and disease. Causal frameworks, such as Mendelian randomization (MR), provide a foundation to begin integrating data for new biological discoveries. Despite the growing number of MR applications in a wide variety of biomedical studies, there are few approaches for the systematic analysis of omic data. The large number and diverse types of molecular components involved in complex diseases interact through complex networks, and classical MR approaches targeting individual components do not consider the underlying relationships. In contrast, causal network models established in the principles of MR offer significant improvements to the classical MR framework for understanding omic data. Integration of these mostly distinct branches of statistics is a recent development, and we here review the current progress. To set the stage for causal network models, we review some recent progress in the classical MR framework. We then explain how to transition from the classical MR framework to causal networks. We discuss the identification of causal networks and evaluate the underlying assumptions. We also introduce some tests for sensitivity analysis and stability assessment of causal networks. We then review practical details to perform real data analysis and identify causal networks and highlight some of the utility of causal networks. The utilities with validated novel findings reveal the full potential of causal networks as a systems approach that will become necessary to integrate large-scale omic data.

Keywords: causal networks; classical MR; multiomic integration; principles of mendelian randomization; stability of causal networks; systems approach; systems biology.

FIGURE 1

MR applications. (A). Multivariable MR. Multiple $\mathrm{I}\mathrm{V}$ s for multiple explanatory variables of the same response to estimate the direct effect of each explanatory variable on the response. U stands for a set of confounders. (B). Multiple uncorrelated $\mathrm{I}\mathrm{V}$ s. Multiple uncorrelated $\mathrm{I}\mathrm{V}$ s for one explanatory variable to predict significant variation in the explanatory variable, satisfy a robust relationship between the $\mathrm{I}\mathrm{V}$ and the explanatory variable. (C). Two-step MR for mediation analysis. In the case that there is a mediator, considering two $\mathrm{I}\mathrm{V}$ s (one for the explanatory variable and one for the mediator) facilitates measuring the direct effect of the explanatory variable X on the response.

FIGURE 2

Two-sample MR. A diagram representing the application of two-sample MR when data on IV, explanatory variable, and response are not available for all samples. Sample 1 has genetic and explanatory variable records; therefore, we measure the effect size of genetic variants on the explanatory variable. Sample 2 has genetic variant and response records and not explanatory variable measurements, therefore, to estimate the genetic variation of any explanatory variable, we use the effect size from sample 1. Then, we estimate the causal relationship between the genetically estimated explanatory variable and response.

FIGURE 3

A transition from the classical MR framework. Interest is in finding the causal relationship between a metabolite and a lipid where we do not know which one is the response. Two of the possible causal diagrams are represented and each one will be assessed separately to select the most likely causal diagram.

FIGURE 4

Examples for stability tests. (A). To assess the effect of $\left\{X\right\}$ on $\left\{Y\right\}$ in this causal network, there are two equivalent sets of confounders $\{E,Z$ } and $\{F,Z$ }, which means considering either of the sets, the study of the effect $\left\{X\right\}$ on $\left\{Y\right\}$ is unconfounded and the effect does not vary significantly (Confounding-equivalent Test). (B). To assess the effect of $\left\{X\right\}$ on $\left\{Y\right\}$ in this causal network, $\left\{Z\right\}$ is the confounder. Therefore, knowing the value of variable $T$ does not change estimating the effect of $\left\{X\right\}$ on $\left\{Y\right\}$ if we hold the variable $\left\{Z\right\}$ constant.

FIGURE 5

Metabolomic-causal network. (A). In total, 325 polygenic factors satisfied MR assumptions/valid IVs (pale nodes) and were used to facilitate the identification of the causal network of 122 metabolites (orange nodes). (B). A close-up of the network. (C). A part of the network with no genome $IV$ a result, some of the causal relationships are not identified, depicted as bi-directed links. Interestingly, we noticed that the corresponding metabolites are dietary-related metabolites that are mostly influenced by environmental factors and not genetics.

FIGURE 6

Causal Network Parameters. Numbers stand for metabolites, edges for conditional dependence properties, and arrows for causal relationships. (A). Modules. The set of entities that highly interact. The identified modules generally coincide with known pathways. For example, the blue and pink circles consist of related fatty acid and amino acid molecules respectively. (B). Example of a broadcaster. Intervention in broadcasters may change the level in the entire system since they directly or indirectly influence multiple other entities in system. (C). Example of a receptor. The level of receptors may predict the level of the entire system since they capture the effect of multiple other entities.

FIGURE 7

Systematic integration of genetics, metabolomics, and triglycerides. (A). The focus is on the nine metabolites with direct effects on triglycerides as well as some of the indirect effects. For example, no need to know about the levels of choline if we know about glycine levels since the effect of choline on triglycerides is only through glycine. (B). We see that the effect of four metabolites on triglycerides is through arachidonate with the largest effect on triglycerides (Yazdani et al., 2016d).