Activity-driven network modeling and control of the spread of two concurrent epidemic strains

Abstract

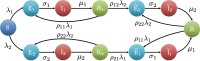
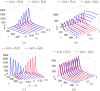
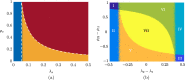
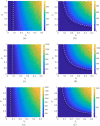
The emergency generated by the current COVID-19 pandemic has claimed millions of lives worldwide. There have been multiple waves across the globe that emerged as a result of new variants, due to arising from unavoidable mutations. The existing network toolbox to study epidemic spreading cannot be readily adapted to the study of multiple, coexisting strains. In this context, particularly lacking are models that could elucidate re-infection with the same strain or a different strain-phenomena that we are seeing experiencing more and more with COVID-19. Here, we establish a novel mathematical model to study the simultaneous spreading of two strains over a class of temporal networks. We build on the classical susceptible-exposed-infectious-removed model, by incorporating additional states that account for infections and re-infections with multiple strains. The temporal network is based on the activity-driven network paradigm, which has emerged as a model of choice to study dynamic processes that unfold at a time scale comparable to the network evolution. We draw analytical insight from the dynamics of the stochastic network systems through a mean-field approach, which allows for characterizing the onset of different behavioral phenotypes (non-epidemic, epidemic, and endemic). To demonstrate the practical use of the model, we examine an intermittent stay-at-home containment strategy, in which a fraction of the population is randomly required to isolate for a fixed period of time.

Keywords: Bi-virus; Complex networks; Control; Epidemics; Temporal network.

Fig. 1

Progression of a virus spread with two strains. The diagram describes the transitions that each individual undergoes between health states. All parameters are constant and represent transition probabilities or rates

Fig. 2

Illustrative example of the time evolution of the epidemic spreading process. Evolution of the epidemic in terms of the total infection counts for strain 1 ($I_1(t)+{\tilde{I}}_1(t)$) and 2 ($I_2(t)+{\tilde{I}}_2(t)$), averaged over 1000 independent Monte Carlo simulations for a different values of ${\lambda }_1$ with ${\lambda }_2=2{\lambda }_1$ being twice infectious than the first variant. Here ${\lambda }_1$ is varied from 0 to 0.2, thus representing cases where both variants are in the non-epidemic regime and transition to an epidemics as ${\lambda }_1$ increases. b Re-infection parameter of the second variant ${\rho }_{22}$ with ${\rho }_{21}={\rho }_{22}$ and ${\lambda }_1={\lambda }_2=0.2$. c ${\lambda }_1$ varies between 0 and 0.5, while ${\lambda }_2=0.5-{\lambda }_1$. d Number of re-infected individuals varying the cross-strain re-infection probability ${\rho }_{12}$ with ${\lambda }_1={\lambda }_2=0.2$

Fig. 3

Two-dimensional diagram illustrating different types of behaviors of the stochastic network systems. In a, the two strains have equal infection and re-infection parameters. We vary the infection parameters ${\lambda }_1={\lambda }_2={\lambda }_s$ on the interval [0, 0.5], while the re-infection parameters ${\rho }_{11}={\rho }_{22}={\rho }_s$ are also varied on the interval [0, 1]. The blue region represents the non-epidemic regime, the orange the epidemic regime, and the red the endemic regime. Dashed lines indicate theoretical predictions. In b, we vary the infection and re-infection parameter values. Specifically, ${\lambda }_1$ and ${\rho }_{11}$ are varied on the interval [0, 0.5] and [0, 1], respectively, while we set ${\lambda }_2=0.5-{\lambda }_1$ and ${\rho }_{22}=1-{\rho }_{11}$. Seven regions are highlighted, depending on the behavior of the two strains. In Region I, strain 1 is non-epidemic and strain 2 is epidemic; in Region II, strain 1 is non-epidemic and strain 2 is endemic; In Region III, strain 2 is non-epidemic and strain 1 is epidemic; In Region IV, strain 2 is non-epidemic and strain 1 is endemic; in Region V, strain 1 is epidemic and strain 2 is endemic; in Region VI, strain 2 is epidemic and strain 1 is endemic; in Region VII, both strains are endemic

Fig. 4

Two-dimensional diagrams illustrating the outcome of the intermittent stay-at-home containment strategy for three different values of the fraction of population: a, b $p=60\%$, c, d $p=50\%$, and e, f $p=30\%$. For each case, we report the peak count of infections (a, c, e) and the steady-state value (b, d, f), as determined from averaging the last 50 time steps. The white-dashed lines represent the stability thresholds computed from Floquet theory and the red dashed lines are stability threshold for $p=0\%$ (absence of the containment strategy, corresponding to Theorems 1 and 2)