A stochastically perturbed co-infection epidemic model for COVID-19 and hepatitis B virus

Abstract

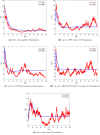
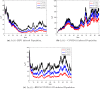
A new co-infection model for the transmission dynamics of two virus hepatitis B (HBV) and coronavirus (COVID-19) is formulated to study the effect of white noise intensities. First, we present the model equilibria and basic reproduction number. The local stability of the equilibria points is proved. Moreover, the proposed stochastic model has been investigated for a non-negative solution and positively invariant region. With the help of Lyapunov function, analysis was performed and conditions for extinction and persistence of the disease based on the stochastic co-infection model were derived. Particularly, we discuss the dynamics of the stochastic model around the disease-free state. Similarly, we obtain the conditions that fluctuate at the disease endemic state holds if $min(R_H^s,R_C^s,R_{\mathrm{HC}}^s)>1$ . Based on extinction as well as persistence some conditions are established in form of expression containing white noise intensities as well as model parameters. The numerical results have also been used to illustrate our analytical results.

Keywords: Extinction; Numerical results; Persistence; Stability analysis; Stochastic co-infection model.

Fig. 1

The detailed flowcharts of COVID-19 and HBV co-infection transmission of system (1)

Fig. 2

The detailed flowcharts of COVID-19 and HBV co-infection transmission of system (2)

Fig. 3

Simulations of $(S(t),I_H(t),I_C(t),I_{\mathit{HC}}(t),R(t))$ for deterministic model (1) and stochastic model (2) with parameters given in Table 2 ($V_1$)

Fig. 4

Simulations of $(S(t),I_H(t),I_C(t),I_{\mathit{HC}}(t),R(t))$ for deterministic model (1) and stochastic model (2) with parameters given in Table 2 ($V_2$)

Fig. 5

Simulations of $(I_H(t),I_C(t),I_{\mathit{HC}})$ for the deterministic and stochastic models, when $I_H(0)=50,I_C(0)=10,I_{\mathit{HC}}=60$ and noises intensity $({\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5)=(0.145,0.350,0.268,0.425,0.110)$

Fig. 6

Simulations of $(I_H(t),I_C(t),I_{\mathit{HC}})$ for the deterministic and stochastic models, when $I_H(0)=50,I_C(0)=10,I_{\mathit{HC}}(0)=60$ and noises intensity $({\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5)=(0.245,0.250,0.250,0.425,0.210)$

Fig. 7

Simulations of $(I_H(t),I_C(t),I_{\mathit{HC}})$ for the deterministic and stochastic models, when $I_H(0)=50,I_C(0)=10,I_{\mathit{HC}}(0)=60$ and noises intensity $({\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5)=(0.205,0.210,0.150,0.425,0.220)$