Systematic description of COVID-19 pandemic using exact SIR solutions and Gumbel distributions

Abstract

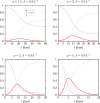
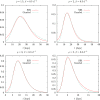
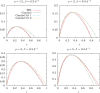
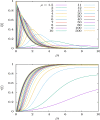
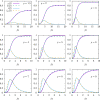
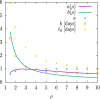
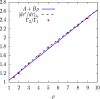
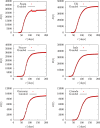
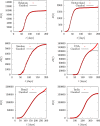
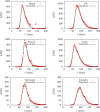
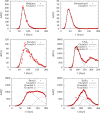
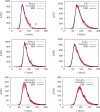
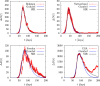
An epidemiological study is carried out in several countries analyzing the first wave of the COVID-19 pandemic using the SIR model and Gumbel distribution. The equations of the SIR model are solved exactly using the proper time as a parameter. The physical time is obtained by integration of the inverse of the infected function over proper time. Some properties of the solutions of the SIR model are studied such as time scaling and the asymmetry, which allows to obtain the basic reproduction number from the data. Approximations to the solutions of the SIR model are studied using Gumbel distributions by least squares fit or by adjusting the maximum of the infected function. Finally, the parameters of the SIR model and the Gumbel function are extracted from the death data and compared for the different countries. It is found that ten of the selected countries are very well described by the solutions of the SIR model, with a basic reproduction number between 3 and 8.

Keywords: COVID-19 coronavirus; Differential equations; Gumbel distribution; SIR model.

Fig. 1

Solution of the SIR equations as a function of proper time $\tau$ for initial susceptible $s_{{}_0}=0.99$ and for several values of the basic reproduction number $\rho ={\mathcal{R}}_0$

Fig. 2

The peak values of i, $\tau$ as a function of the basic reproduction number $\rho$. For $s_{{}_0}=0.99$ the peak values are almost independent of $s_{{}_0}$

Fig. 3

Solution of the SIR equations as a function of physical time, t, for initial susceptible $s_{{}_0}=0.99$, for $\beta =0.3{\text{d}}^{-1}$, and for several values of the reproduction number $\rho ={\mathcal{R}}_0$

Fig. 4

Gumbel distribution compared to the exact Solution of the SIR equations for $s_{{}_0}=0.99$, $\beta =0.3{\text{d}}^{-1}$, and for several values of the reproduction number $\rho$

Fig. 5

Three Gumbel distributions as a function of the proper time, compared to the exact Solution of the SIR equations for $s_{{}_0}=0.99$, $\beta =0.3{\text{d}}^{-1}$, and for several values of the reproduction number $\rho$. The parameters of the Gumbel distributions correspond to the mean-square fit, proper-time fit 1 and proper-time fit 2. In proper-time fit 1, the value of $t_0$ is taken from Table 1

Fig. 6

Three Gumbel distributions compared to the exact Solution of the SIR equations for $s_{{}_0}=0.99$, $\beta =0.3{\text{d}}^{-1}$, and for several values of the basic reproduction number $\rho$. The parameters of the Gumbel distributions correspond to the mean-square fit, proper-time fit 1 and proper-time fit 2. In proper-time fit 1, the value of $t_0$ is taken from Table 1

Fig. 7

Solutions of the SIR equations for values of the basic reproduction number $\rho$ from 1.5 to 500. The functions i(t) and $\tau (t)=r(t)$ are Plotted as a function of the normalized time $\beta t$

Fig. 8

Solutions of the SIR equations for several values of the basic reproduction number $\rho$, and for $s_{{}_0}=0.99$. The functions i(t) and $\tau (t)=r(t)$ are plotted as a function of the normalized time $\beta t$. These are compared to the approximate solution obtained with a Gumbel function G(t) fitted to $\tau (t)$, and with the corresponding infected function $i_G(t)=1-G(t)-s_{{}_0}exp(-\rho G(t))$ of the extended SIR model

Fig. 9

Parameters of the Gumbel function G(t) fitted to $\tau (t)$ in Fig. 8. These are compared to the functions $a(\rho )$ and $b(\rho )$ from Eqs. (39, 40)

Fig. 10

Asymmetry of the SIR solutions as a function of $\rho$. The points are the values of the asymmetry computed numerically for discrete values of $\rho =1.5,2,3,\dots ,9$. The solid line is a fitted right line $A+B\rho$. The dashed line is the Jacobian $|\mathrm{d}{\tau }^{\prime }{/\mathrm{d}\tau |}_{i_{{}_0}}$ evaluated for $i_{{}_0}=0.84i_{\mathrm{peak}}$

Fig. 11

The function i(t) obtained for $\rho =3$, and computed for different initial values of i(0)

Fig. 12

Total deaths D(t) during the first wave of the COVID-19 pandemic for several countries, compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 13

Total deaths D(t) during the first wave of the COVID-19 pandemic for several countries, compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 14

Daily deaths $\mathrm{\Delta }D(t)$ during the first wave of the COVID-19 pandemic for several countries compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 15

Daily deaths $\mathrm{\Delta }D(t)$ during the first wave of the COVID-19 pandemic for several countries compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 16

Daily deaths $\mathrm{\Delta }D(t)$ during the first wave of the COVID-19 pandemic for several countries compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 17

Daily deaths $\mathrm{\Delta }D(t)$ in the first wave of coronavirus pandemic for several countries, compared to the Gumbel function G(t). The parameter b of the Gumbel function fitted to the data is given in Table 2. Data are from Ref. [49]

Fig. 18

Locations of the different countries studied in the plane of SIR parameters $(\rho ,1/\beta )$