Concentration fluctuations in growing and dividing cells: Insights into the emergence of concentration homeostasis
- PMID: 36194626
- PMCID: PMC9565450
- DOI: 10.1371/journal.pcbi.1010574
Concentration fluctuations in growing and dividing cells: Insights into the emergence of concentration homeostasis
Abstract
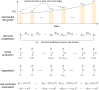
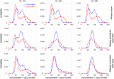
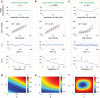
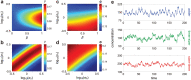
Intracellular reaction rates depend on concentrations and hence their levels are often regulated. However classical models of stochastic gene expression lack a cell size description and cannot be used to predict noise in concentrations. Here, we construct a model of gene product dynamics that includes a description of cell growth, cell division, size-dependent gene expression, gene dosage compensation, and size control mechanisms that can vary with the cell cycle phase. We obtain expressions for the approximate distributions and power spectra of concentration fluctuations which lead to insight into the emergence of concentration homeostasis. We find that (i) the conditions necessary to suppress cell division-induced concentration oscillations are difficult to achieve; (ii) mRNA concentration and number distributions can have different number of modes; (iii) two-layer size control strategies such as sizer-timer or adder-timer are ideal because they maintain constant mean concentrations whilst minimising concentration noise; (iv) accurate concentration homeostasis requires a fine tuning of dosage compensation, replication timing, and size-dependent gene expression; (v) deviations from perfect concentration homeostasis show up as deviations of the concentration distribution from a gamma distribution. Some of these predictions are confirmed using data for E. coli, fission yeast, and budding yeast.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

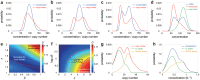
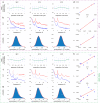
Similar articles
-
Analysis of Noise Mechanisms in Cell-Size Control.Biophys J. 2017 Jun 6;112(11):2408-2418. doi: 10.1016/j.bpj.2017.04.050. Biophys J. 2017. PMID: 28591613 Free PMC article.
-
From noisy cell size control to population growth: When variability can be beneficial.Phys Rev E. 2025 Mar;111(3-1):034407. doi: 10.1103/PhysRevE.111.034407. Phys Rev E. 2025. PMID: 40247490
-
Characterizing non-exponential growth and bimodal cell size distributions in fission yeast: An analytical approach.PLoS Comput Biol. 2022 Jan 18;18(1):e1009793. doi: 10.1371/journal.pcbi.1009793. eCollection 2022 Jan. PLoS Comput Biol. 2022. PMID: 35041656 Free PMC article.
-
How do fission yeast cells grow and connect growth to the mitotic cycle?Curr Genet. 2017 May;63(2):165-173. doi: 10.1007/s00294-016-0632-0. Epub 2016 Jul 27. Curr Genet. 2017. PMID: 27465359 Review.
-
Regularities and irregularities in the cell cycle of the fission yeast, Schizosaccharomyces pombe (a review).Acta Microbiol Immunol Hung. 2002;49(2-3):289-304. doi: 10.1556/AMicr.49.2002.2-3.17. Acta Microbiol Immunol Hung. 2002. PMID: 12109161 Review.
Cited by
-
What can we learn when fitting a simple telegraph model to a complex gene expression model?PLoS Comput Biol. 2024 May 14;20(5):e1012118. doi: 10.1371/journal.pcbi.1012118. eCollection 2024 May. PLoS Comput Biol. 2024. PMID: 38743803 Free PMC article.
-
Solving stochastic gene-expression models using queueing theory: A tutorial review.Biophys J. 2024 May 7;123(9):1034-1057. doi: 10.1016/j.bpj.2024.04.004. Epub 2024 Apr 9. Biophys J. 2024. PMID: 38594901 Free PMC article. Review.
-
Stochastic gene expression in proliferating cells: Differing noise intensity in single-cell and population perspectives.PLoS Comput Biol. 2025 Jun 10;21(6):e1013014. doi: 10.1371/journal.pcbi.1013014. eCollection 2025 Jun. PLoS Comput Biol. 2025. PMID: 40493721 Free PMC article.
-
Homeostasis of mRNA concentrations through coupling transcription, export, and degradation.iScience. 2024 Jul 18;27(8):110531. doi: 10.1016/j.isci.2024.110531. eCollection 2024 Aug 16. iScience. 2024. PMID: 39175768 Free PMC article.
-
Stochastic Gene Expression in Proliferating Cells: Differing Noise Intensity in Single-Cell and Population Perspectives.bioRxiv [Preprint]. 2024 Jun 29:2024.06.28.601263. doi: 10.1101/2024.06.28.601263. bioRxiv. 2024. Update in: PLoS Comput Biol. 2025 Jun 10;21(6):e1013014. doi: 10.1371/journal.pcbi.1013014. PMID: 38979195 Free PMC article. Updated. Preprint.
References
-
- Peccoud J, Ycart B. Markovian modeling of gene-product synthesis. Theor Popul Biol. 1995;48(2):222–234. doi: 10.1006/tpbi.1995.1027 - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

