Machine learning classification reveals robust morphometric biomarker of glial and neuronal arbors

Abstract

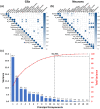
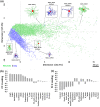
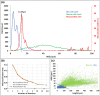
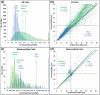
Neurons and glia are the two main cell classes in the nervous systems of most animals. Although functionally distinct, neurons and glia are both characterized by multiple branching arbors stemming from the cell bodies. Glial processes are generally known to form smaller trees than neuronal dendrites. However, the full extent of morphological differences between neurons and glia in multiple species and brain regions has not yet been characterized, nor is it known whether these cells can be reliably distinguished based on geometric features alone. Here, we show that multiple supervised learning algorithms deployed on a large database of morphological reconstructions can systematically classify neuronal and glial arbors with nearly perfect accuracy and precision. Moreover, we report multiple morphometric properties, both size related and size independent, that differ substantially between these cell types. In particular, we newly identify an individual morphometric measurement, Average Branch Euclidean Length that can robustly separate neurons from glia across multiple animal models, a broad diversity of experimental conditions, and anatomical areas, with the notable exception of the cerebellum. We discuss the practical utility and physiological interpretation of this discovery.

Keywords: K-nearest neighbor; NeuroMorpho.Org; branch length; cellular identity; morphology; neuroinformatics; random forest; supervised learning; support vector machine; tree size.

FIGURE 1

Representative diversity of morphological reconstructions of glia and neurons from NeuroMorpho.Org with labels indicating animal species, anatomical region, and cell type. Blue: Glial processes; green: Neuronal dendrites; red: Cell bodies.

FIGURE 2

Distribution of (a) animal species and (b) brain regions for the analyzed glia and neuron datasets.

FIGURE 3

Schematic of selected morphometric features. (a) Illustration of width, depth, and maximum Euclidean distance (left) in a monkey neocortical pyramidal cell (NMO_00002) from the Wearne_Hof archive (Duan et al., 2002); and of height and fragmentation (right) in a hippocampal granule cell (NMO_73103) from the Diaz archive (Sebastián‐Serrano et al., 2016). (b) Diameter and local or remote bifurcation amplitude (left) in a rat neocortical microglia (NMO_95641) from the Roysam archive (Megjhani et al., 2015); and maximum path distance, length, and number of branches, bifurcations, and stems in a rat cortical oligodendrocyte (NMO_131081) from the Sato_Bigbee archive (Mohamed et al., 2020).

FIGURE 4

Orthogonalization of morphometric features. (a) Correlation matrix quantifying the interdependence among 19 morphometric features of glia and of (b) neurons. The coefficient of determination (R ²) is shown on a dark intensity scale. (c) Scree plot of the variance contributed by each sequential principal component (blue bars, left axis) and the corresponding cumulative distribution (red line, right axis).

FIGURE 5

(a) PCA biplot of the two‐dimensional distribution of neurons and glia relative to the first two principal components (PC1 and PC2). Morphological tracings of several cells (glia: Blue; neurons: Green) are also shown to illustrate their structural variability and similarity in this space. (b) Linear contributions of all morphometric parameters to PC1 and (c) PC2. Negative loadings indicate a high weight of the scale low‐end for a parameter; for instance, cells with large positive PC2 values tend to have very few branches, whereas cells with many branches tend to have large negative PC2 values.

FIGURE 6

Classification performance for support vector machine (SVM), K‐nearest neighbors (KNN), and random Forest (RF), including the area under the curve (AUC) of the receiver‐operating characteristic plot.

FIGURE 7

Silhouette profiles of length, height, contraction, number of branches, and average branch Euclidean length (ABEL) of glia and neurons, and examples of branch Euclidean length measurements from a rat basal ganglia GABAergic cell (NMO_68194) from the Smith archive (Smith et al., 2015).

FIGURE 8

Classification performance of average branch Euclidean length (ABEL). (a) ABEL distributions of neurons (green), glia (blue), and cells that are misclassified (red, secondary axis) based on optimal separation threshold of 14.33 μm (vertical dashed line). (b) Misclassification rate as a function of the number of branches sampled to estimate ABEL. (c) Linear separation (black dashed line) between neurons (green) and glia (blue) on the plane defined by arbor height and ABEL.

FIGURE 9

Relationship between the average branch Euclidean length (ABEL) of terminal branches and internal (bifurcating) branches for glia (blue) and neurons (green). (a) Distribution of the ratio between terminal and internal ABEL, with medians (vertical dotted lines) and means (vertical dashed lines) indicated. (b) 2D scatter and linear regression between terminal ABEL and all‐branch ABEL, with respective classification thresholds indicated by horizontal and vertical dashed lines. (c) Same as A except limited to cells that are misclassified based on all‐branch ABEL. (d) Same as B except limited to cells that are misclassified based on all‐branch ABEL. The filled circles represent the subset of neurons and glia that are misclassified based on all‐branch ABEL but correctly classified based on terminal ABEL. An even larger number of cells (not shown) are correctly classified based on all‐branch ABEL but misclassified based on terminal ABEL.

FIGURE 10

Classification of glia and neurons across anatomical regions. (a) Number of cells analyzed (stacked blue bars, right axis: Main dataset, solid; and additional dataset, striped) and classification accuracy (black line and red triangle, left axis). (b) ABEL distribution of cerebellar glia. Cells to the right of the threshold (vertical dashed line) are misclassified. (c) ABEL distribution of cerebellar neurons. Cells to the left of the threshold (vertical dashed line) are misclassified.