EpiLPS: A fast and flexible Bayesian tool for estimation of the time-varying reproduction number

Abstract

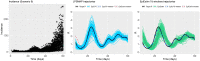
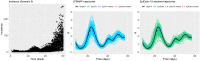
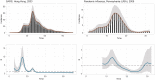
In infectious disease epidemiology, the instantaneous reproduction number [Formula: see text] is a time-varying parameter defined as the average number of secondary infections generated by an infected individual at time t. It is therefore a crucial epidemiological statistic that assists public health decision makers in the management of an epidemic. We present a new Bayesian tool (EpiLPS) for robust estimation of the time-varying reproduction number. The proposed methodology smooths the epidemic curve and allows to obtain (approximate) point estimates and credible intervals of [Formula: see text] by employing the renewal equation, using Bayesian P-splines coupled with Laplace approximations of the conditional posterior of the spline vector. Two alternative approaches for inference are presented: (1) an approach based on a maximum a posteriori argument for the model hyperparameters, delivering estimates of [Formula: see text] in only a few seconds; and (2) an approach based on a Markov chain Monte Carlo (MCMC) scheme with underlying Langevin dynamics for efficient sampling of the posterior target distribution. Case counts per unit of time are assumed to follow a negative binomial distribution to account for potential overdispersion in the data that would not be captured by a classic Poisson model. Furthermore, after smoothing the epidemic curve, a "plug-in'' estimate of the reproduction number can be obtained from the renewal equation yielding a closed form expression of [Formula: see text] as a function of the spline parameters. The approach is extremely fast and free of arbitrary smoothing assumptions. EpiLPS is applied on data of SARS-CoV-1 in Hong-Kong (2003), influenza A H1N1 (2009) in the USA and on the SARS-CoV-2 pandemic (2020-2021) for Belgium, Portugal, Denmark and France.

Fig 1

Illustration of smoothing windows of width ω to estimate ${\mathcal{R}}_t$ with EpiEstim. (a) Cori et al. (2013) [3] convention with sliding windows [t − ω; t], where ${\mathcal{R}}_t$ is reported at the end of the window. (b) Gostic et al. (2020) [2] recommendation with centered sliding windows [t − ω/2; t + ω/2], where ${\mathcal{R}}_t$ is reported at the midpoint of the window. Under the midpoint rule, ${\mathcal{R}}_t$ estimates for the last ω/2 time units are unavailable ∅.

Fig 2

(Left) Simulated incidence data for Scenario 2. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the end of the window. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 3

(Left) Simulated incidence data for Scenario 3. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the end of the window. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 4

(Left) Simulated incidence data for Scenario 9. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the end of the window. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 5

(Left) Simulated incidence data for Scenario 2. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the window midpoint. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 6

(Left) Simulated incidence data for Scenario 3. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the window midpoint. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 7

(Left) Simulated incidence data for Scenario 9. (Center) Estimated trajectories of ${\mathcal{R}}_t$ for each simulated dataset with LPSMAP. (Right) Estimated trajectories of ${\mathcal{R}}_t$ with EpiEstim using weekly sliding windows and ${\mathcal{R}}_t$ reported at the window midpoint. The pointwise median estimate of ${\mathcal{R}}_t$ for EpiLPS (dashed) and EpiEstim (dotted) is also shown.

Fig 8. Real-time properties of EpiLPS (top) and EpiEstim (bottom) when applied on domains T=[1,T] and T*=[1,T+1].

EpiLPS provides real-time estimates of ${\mathcal{R}}_t$ only at the boundary of the considered domain and estimates at preceding time points are retrospective. On the contrary, estimates of ${\mathcal{R}}_t$ with EpiEstim are always real-time and therefore preferred for a timely usage.

Fig 9

(Left column) EpiLPS fit for the epidemic curve (top) and the instantaneous reproduction number ${\mathcal{R}}_t$ (bottom) of the SARS outbreak in Hong Kong, 2003. (Right column) EpiLPS fit for the epidemic curve (top) and the instantaneous reproduction number ${\mathcal{R}}_t$ (bottom) of the pandemic influenza in Pennsylvania, 2009. The shaded area corresponds to the 95% credible interval at each day.

Fig 10. Estimated reproduction number from 2020–04-05 to 2021–10-31 for Belgium, Denmark, Portugal and France with LPSMAP using K = 30 B-splines and a second-order penalty.

The shaded area corresponds to the 95% credible interval at each day. Dashed curves are results obtained with EpiEstim (with weekly sliding windows and estimated ${\mathcal{R}}_t$ reported at the end of the window).