Mathematical model for the novel coronavirus (2019-nCOV) with clinical data using fractional operator
- PMID: 36245569
- PMCID: PMC9537912
- DOI: 10.1002/num.22915
Mathematical model for the novel coronavirus (2019-nCOV) with clinical data using fractional operator
Abstract
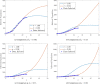
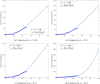
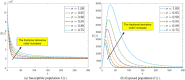
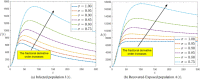
Coronavirus infection (COVID-19) is a considerably dangerous disease with a high demise rate around the world. There is no known vaccination or medicine until our time because the unknown aspects of the virus are more significant than our theoretical and experimental knowledge. One of the most effective strategies for comprehending and controlling the spread of this epidemic is to model it using a powerful mathematical model. However, mathematical modeling with a fractional operator can provide explanations for the disease's possibility and severity. Accordingly, basic information will be provided to identify the kind of measure and intrusion that will be required to control the disease's progress. In this study, we propose using a fractional-order SEIARPQ model with the Caputo sense to model the coronavirus (COVID-19) pandemic, which has never been done before in the literature. The stability analysis, existence, uniqueness theorems, and numerical solutions of such a model are displayed. All results were numerically simulated using MATLAB programming. The current study supports the applicability and influence of fractional operators on real-world problems.
Keywords: Adams–Bashforth–Moulton method; COVID‐19 disease; existence theorems; numerical simulations; stability analysis; uniqueness theorems.
© 2022 Wiley Periodicals LLC.
Figures
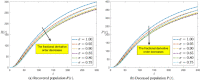
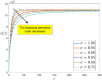
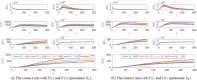
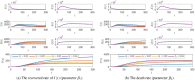


Similar articles
-
Dynamics of a fractional order mathematical model for COVID-19 epidemic transmission.Physica A. 2023 Jan 1;609:128383. doi: 10.1016/j.physa.2022.128383. Epub 2022 Dec 5. Physica A. 2023. PMID: 36506918 Free PMC article.
-
A hybrid fractional optimal control for a novel Coronavirus (2019-nCov) mathematical model.J Adv Res. 2021 Sep;32:149-160. doi: 10.1016/j.jare.2020.08.006. Epub 2020 Aug 25. J Adv Res. 2021. PMID: 32864171 Free PMC article.
-
A study on fractional HBV model through singular and non-singular derivatives.Eur Phys J Spec Top. 2022;231(10):1885-1904. doi: 10.1140/epjs/s11734-022-00460-6. Epub 2022 Mar 2. Eur Phys J Spec Top. 2022. PMID: 35251498 Free PMC article.
-
Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach.Chaos Solitons Fractals. 2022 Feb;155:111636. doi: 10.1016/j.chaos.2021.111636. Epub 2021 Nov 27. Chaos Solitons Fractals. 2022. PMID: 34866811 Free PMC article.
-
Fractional Model and Numerical Algorithms for Predicting COVID-19 with Isolation and Quarantine Strategies.Int J Appl Comput Math. 2021;7(4):142. doi: 10.1007/s40819-021-01086-3. Epub 2021 Jun 30. Int J Appl Comput Math. 2021. PMID: 34226872 Free PMC article.
Cited by
-
A fractional mathematical model with nonlinear partial differential equations for transmission dynamics of severe acute respiratory syndrome coronavirus 2 infection.Healthc Anal (N Y). 2023 Dec;4:100209. doi: 10.1016/j.health.2023.100209. Epub 2023 Jun 12. Healthc Anal (N Y). 2023. PMID: 37377904 Free PMC article.
References
-
- Keeling M. J. and Rohani P., Modeling infectious diseases in humans and animals, Princeton University Press, Princeton, NJ, 2011.
-
- Waziri A., Massawe E., and Makinde O., Mathematical modelling of HIV/AIDS dynamics with treatment and vertical transmission, Appl. Math. 2 (2012), 77–89.
LinkOut - more resources
Full Text Sources
