Optimal control strategies for the reliable and competitive mathematical analysis of Covid-19 pandemic model

Abstract

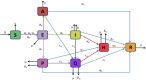
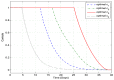
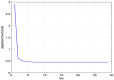
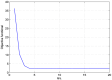
To understand dynamics of the COVID-19 disease realistically, a new SEIAPHR model has been proposed in this article where the infectious individuals have been categorized as symptomatic, asymptomatic, and super-spreaders. The model has been investigated for existence of a unique solution. To measure the contagiousness of COVID-19, reproduction number $R_0$ is also computed using next generation matrix method. It is shown that the model is locally stable at disease-free equilibrium point when $R_0<1$ and unstable for $R_0>1$ . The model has been analyzed for global stability at both of the disease-free and endemic equilibrium points. Sensitivity analysis is also included to examine the effect of parameters of the model on reproduction number $R_0$ . A couple of optimal control problems have been designed to study the effect of control strategies for disease control and eradication from the society. Numerical results show that the adopted control approaches are much effective in reducing new infections.

Keywords: COVID‐19; Optimal control; Pontryagin maximum principle; existence and uniqueness; local and global stabilities; nonpharmaceutical; sensitivity analysis.

FIGURE 1

Flow diagram of Covid‐19 disease transmission [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2

Flow diagram of Covid‐19 disease transmission with quarantine class [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 3

Optimal controls (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4

Cost functional (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 5

State variables before and after optimization (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 6

Optimal controls (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 7

Cost functional (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 8

State variables before and after optimization (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 9

Flow diagram of Covid‐19 disease transmission with nonpharmaceutical control parameters [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 10

Optimal controls (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 11

Cost functional (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 12

State variables before and after optimization (Case 1) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 13

Optimal controls (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 14

Cost functional (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 15

State variables before and after optimization (Case 2) [Colour figure can be viewed at wileyonlinelibrary.com]