A new computational model illuminates the extraordinary eyes of Phronima

Abstract

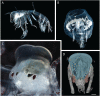
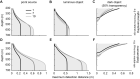
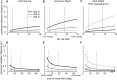
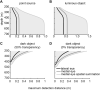
Vision in the midwater of the open ocean requires animals to perform visual tasks quite unlike those of any other environment. These tasks consist of detecting small, low contrast objects and point sources against a relatively dim and uniform background. Deep-sea animals have evolved many extraordinary visual adaptations to perform these tasks. Linking eye anatomy to specific selective pressures, however, is challenging, not least because of the many difficulties of studying deep-sea animals. Computational modelling of vision, based on detailed morphological reconstructions of animal eyes, along with underwater optics, offers a chance to understand the specific visual capabilities of individual visual systems. Prior to the work presented here, comprehensive models for apposition compound eyes in the mesopelagic, the dominant eye form of crustaceans, were lacking. We adapted a model developed for single-lens eyes and used it to examine how different parameters affect the model's ability to detect point sources and extended objects. This new model also allowed us to examine spatial summation as a means to improve visual performance. Our results identify a trade-off between increased depth range over which eyes function effectively and increased distance at which extended objects can be detected. This trade-off is driven by the size of the ommatidial acceptance angle. We also show that if neighbouring ommatidia have overlapping receptive fields, spatial summation helps with all detection tasks, including the detection of bioluminescent point sources. By applying our model to the apposition compound eyes of Phronima, a mesopelagic hyperiid amphipod, we show that the specialisations of the large medial eyes of Phronima improve both the detection of point sources and of extended objects. The medial eyes outperformed the lateral eyes at every modelled detection task. We suggest that the small visual field size of Phronima's medial eyes and the strong asymmetry between the medial and lateral eyes reflect Phronima's need for effective vision across a large depth range and its habit of living inside a barrel. The barrel's narrow aperture limits the usefulness of a large visual field and has allowed a strong asymmetry between the medial and lateral eyes. The model provides a useful tool for future investigations into the visual abilities of apposition compound eyes in the deep sea.

Fig 1. Phronima exemplars.

(A) Lateral view of Phronima’s body with head at left. (B) Female Phronima in barrel with brood. (C) Close-up of Phronima’s eyes with their medial eye retinas visible at the base of their long light guides and the lateral eye retinas visible just lateral to them, closely surrounded by the distinguishable corneal lenses of the ommatidia. The lenses of the medial eyes cover the dorsal surface of the head seen as two bulges at the top of the photo. (D) Three-dimensional reconstructions of the medial and lateral eyes based on micro-computed tomography (micro-CT) image data of Specimen 2. Blue and red shading identify the medial and lateral eyes, respectively. The reconstruction was made using Dragonfly (Object Research Systems, Inc.). Scale bar 1 mm.

Fig 2. The sensitivity of ommatidia to point sources.

(A) The receptive fields of target channels comprising either one ommatidium (upper panel) or seven ommatidia (lower panel) viewing a point source (small point depicted above receptive field). Grey levels represent the relative sensitivity of the receptive fields (darker indicating greater sensitivity) and the c-to-c dashed line represents the cross section through which the spatial sensitivity distributions shown in (B) relate. (B) Relative sensitivity of the ommatidia of target channels along the cross sections c-to-c in (A), showing the receptive fields of target channels comprising one ommatidium (upper panel) and seven ommatidia (lower panel). In the upper panel the relative sensitivity of the receptive field to the point source is denoted by S₁ and in the lower panel the relative sensitivity of ommatidium number two to the point source (see inset in the panel) is denoted by S₂. The hexagonal array inset in both panels shows the ommatidia that are included in the target channel. (C) The receptive fields of target channels comprising either one ommatidium (upper panel) or seven ommatidia (lower panel) viewing multiple point sources across a transparent object (the extended luminous object; multiple point sources represented by small points encased in black circle above receptive fields). The inset in (C) shows the point source labels as used in (D). (D) Relative sensitivity of ommatidia in the target channels along the cross sections c-to-c in (C), showing the receptive fields of target channels comprising one ommatidium (upper panel) and seven ommatidia (lower panel). In both panels of figure (D) the relative sensitivity of the receptive field to point sources one, two and three is denoted by SP₁, SP₂, and SP₃, but in the lower panel it is denoted for the receptive field of ommatidium five (see inset in the panel) only. The hexagonal array inset in both panels shows the ommatidia that are included in the target channel.

Fig 3

The receptive fields of target channels comprising (A) a single ommatidium or (C) seven summated ommatidia viewing an extended dark object against background radiance. (B, D) Top-down views of the receptive fields in (A) and (C) showing the object obscuring parts of the receptive field (black circle) and the remaining parts of the receptive field that view the background. Grey levels represent the relative sensitivity of the receptive fields (darker indicating greater sensitivity).

Fig 4. Micro-CT section image of the medial eye of P. sedentaria showing the distal crystalline cone abutting the long light guide proximally.

The two marked points, one central on the cornea and the other at the junction between the crystalline cone and the light guide, determine the optical axis of the ommatidium.

Fig 5. The effects of anatomical parameters on detection distances of three targets against downwelling radiance modelled across depths.

Rows show the effects of increasing or decreasing the test parameter by a factor of two on the maximum detection distance. (A–C) facet diameter, (D–F) quantum efficiency or integration time (exactly equivalent effects), and (G–I) acceptance angle of the ommatidium. Columns show the model results for (A, D, G) a point source, (B, E, H) an extended luminous object, and (C, F, I) an extended dark object with 50% transparency. Extended objects were 1 cm in diameter. Results for an extended dark object with 0% transparency are given in S2 Fig. The thickest black line in each figure shows the result from the average medial eye parameters based on our Phronima specimens (Table 2). The thinner black lines bounding the shaded areas show the result of decreasing (dark grey) or increasing (light grey) the parameters by a factor of two. Note the different scale of the x-axis for different targets.

Fig 6. Visual detection distance across depths showing the effect of spatially summating different numbers of ommatidia in eyes with different sampling arrangements.

Rows show the maximum detection distances of eyes that employ spatial summation and either (A–C) optimally sample visual space (Δρ:Δϕ = 1) or (D–F) oversample visual space (Δρ:Δϕ = 2.4). Each column shows the model results for (A, D) a point source, (B, E) an extended luminous object, and (C, F) an extended dark object. Extended objects were 1 cm in diameter. All targets were viewed against downwelling radiance at different depths. In all figures, the model results are shown for a single ommatidium (black), seven spatially summated ommatidia (dark grey), and 19 spatially summated ommatidia (light grey). Grey shading shows the distances and depths at which detection can occur. Model inputs were those of the medial eyes of Phronima (Table 2) and model parameters (Table 1).

Fig 7. Effect of overlap of ommatidial receptive fields on detection distances and the size of visual field.

(A-C) Increasing overlap always improved maximum detection distance for all targets. (D-E) However, there is a clear trade-off between detection distance and the size of field of view due to ommatidial overlap. Columns show the model results for the detection of a point source (A, D), an extended luminous object (B, E), and an extended dark object (C, F). The number of ommatidia summating in a single channel was calculated as a function of Δρ:Δϕ ratio [10]. For overlaps greater than 16, there are not enough ommatidia within an eye of Phronima to from two distinct channel. The size of the field of view and the receptive field size of the target channel were calculated using the derivations shown in the S3 Appendix. The acceptance angle was taken from the medial eyes of Phronima, 3.9° (Table 2), and we varied the interommatidial angle (from 0.26 to 3.9°) to model different Δρ:Δϕ ratios. Dotted vertical lines show the overlap measured in our Phronima specimens (Δρ:Δϕ = 2.4) and dashed vertical lines show the overlap measured by Land [6] (Δρ:Δϕ = 9.2). Small circles in (D-F) shows Δρ:Δϕ ratios of 1, 5 and 15.

Fig 8. Comparison of detection abilities between the lateral and medial eyes of Phronima.

Model results for the detection distances for (A) the point source, (B) the extended luminous object, and the extended dark object with (C) 50% and (D) 0% transparency. Luminous objects were modelled against horizontal radiance and the dark objects were modelled against downwelling radiance. In all figures we show results for the lateral (black) and medial (dark grey) eyes of Phronima, as well as the medial eyes with spatial summation of 19 ommatidia (light grey). Grey shading shows the distances and depths at which detection can occur.

Fig 9. With increasing depth, more transparent objects become more difficult to detect.

Model results for the lateral and medial eyes of Phronima for detection distances of extended dark objects with different transparencies at (A) 200 m (B) 300 m and (C) 400 m depth. Objects were modelled against downwelling radiance. In all figures we show results for the lateral (black) and medial (dark grey) eyes of Phronima, as well as the medial eyes with spatial summation of 19 ommatidia (light grey). Grey shading shows the distances and transparencies at which detection can occur.