The role of super-spreaders in modeling of SARS-CoV-2
- PMID: 36267691
- PMCID: PMC9558769
- DOI: 10.1016/j.idm.2022.10.003
The role of super-spreaders in modeling of SARS-CoV-2
Abstract
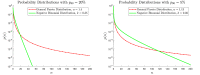
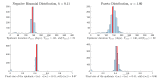
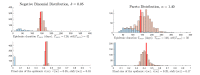
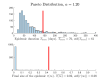
In stochastic modeling of infectious diseases, it has been established that variations in infectivity affect the probability of a major outbreak, but not the shape of the curves during a major outbreak, which is predicted by deterministic models (Diekmann et al., 2012). However, such conclusions are derived under idealized assumptions such as the population size tending to infinity, and the individual degree of infectivity only depending on variations in the infectiousness period. In this paper we show that the same conclusions hold true in a finite population representing a medium size city, where the degree of infectivity is determined by the offspring distribution, which we try to make as realistic as possible for SARS-CoV-2. In particular, we consider distributions with fat tails, to incorporate the existence of super-spreaders. We also provide new theoretical results on convergence of stochastic models which allows to incorporate any offspring distribution with a finite variance.
Keywords: COVID-19; Compartmental models; Offspring distribution for SARS-CoV-2; SEIR; SIR.
© 2022 The Authors.
Conflict of interest statement
All authors declare no competing interests.
Figures

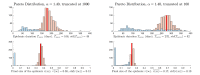
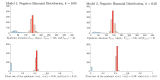
References
-
- Adam D.C., Wu P., Wong J.Y., Lau E.H., Tsang T.K., Cauchemez S., Leung G.M., Cowling B.J. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nature Medicine. 2020;26(11):1714–1719. - PubMed
-
- Andersson H., Britton T. Vol. 151. Springer Science & Business Media; 2012. (Stochastic epidemic models and their statistical analysis).
-
- Armbruster B., Beck E. Elementary proof of convergence to the mean-field model for the sir process. Journal of Mathematical Biology. 2017;75(2):327–339. - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous

