Accommodating site variation in neuroimaging data using normative and hierarchical Bayesian models

Abstract

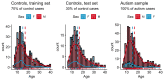
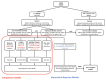
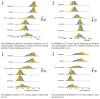
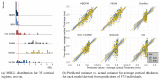
The potential of normative modeling to make individualized predictions from neuroimaging data has enabled inferences that go beyond the case-control approach. However, site effects are often confounded with variables of interest in a complex manner and can bias estimates of normative models, which has impeded the application of normative models to large multi-site neuroimaging data sets. In this study, we suggest accommodating for these site effects by including them as random effects in a hierarchical Bayesian model. We compared the performance of a linear and a non-linear hierarchical Bayesian model in modeling the effect of age on cortical thickness. We used data of 570 healthy individuals from the ABIDE (autism brain imaging data exchange) data set in our experiments. In addition, we used data from individuals with autism to test whether our models are able to retain clinically useful information while removing site effects. We compared the proposed single stage hierarchical Bayesian method to several harmonization techniques commonly used to deal with additive and multiplicative site effects using a two stage regression, including regressing out site and harmonizing for site with ComBat, both with and without explicitly preserving variance caused by age and sex as biological variation of interest, and with a non-linear version of ComBat. In addition, we made predictions from raw data, in which site has not been accommodated for. The proposed hierarchical Bayesian method showed the best predictive performance according to multiple metrics. Beyond that, the resulting z-scores showed little to no residual site effects, yet still retained clinically useful information. In contrast, performance was particularly poor for the regression model and the ComBat model in which age and sex were not explicitly modeled. In all two stage harmonization models, predictions were poorly scaled, suffering from a loss of more than 90% of the original variance. Our results show the value of hierarchical Bayesian regression methods for accommodating site variation in neuroimaging data, which provides an alternative to harmonization techniques. While the approach we propose may have broad utility, our approach is particularly well suited to normative modeling where the primary interest is in accurate modeling of inter-subject variation and statistical quantification of deviations from a reference model.

Keywords: Hierarchical bayesian modeling; Neuroimaging; Normative modeling; Site effects.

Figure 1. Site effects in 573 healthy individuals from the ABIDE data set.

Figure 2. Overview over phenotypic information in the ABIDE data set.

Controls: Age male subjects: M = 17.5., SD = 8.3. Age female subjects: M = 15.6, SD = 7.0., range = 6.5-40; Autism sample: Age male subjects: M = 16.9., SD = 6.5. Age female subjects: M = 15.1, SD = 5.8., range = 8-39;

Figure 3. Pipelines for hierarchical Bayesian and comparison models

Figure 4. Performance measures

Figure 5. Mean standardized log loss and predicted variance for 35 cortical regions.

Figure 6. Forrest plots indicating the heterogeneity between sites

Uncorrected (6a - 6c), corrected with HBLM (6d - 6f) and corrected with HBGPM (6g -6i). Also note the difference in range along the x-axes.

Figure 7. Region specific prevalence of atypical z-scores, control test set.

Prevalence values of individuals with a z -score of ± 2SD, for the HBLM and the HBGPM model. Scores are thresholded at 5%, which is the expected amount of z-scores of ± 2SD within a normative model

Figure 8. Region specific prevalence of atypical z-scores, autism test set.

Prevalence values of individuals with a z -score of ± 2SD, for the HBLM and the HBGPM model. Scores are thresholded at 5%, which is the expected amount of z-scores of ± 2SD within a normative model

Figure 9. Prevalence of atypical z-scores across all regions