Multi-scale mechanobiological model for skeletal muscle hypertrophy

Abstract

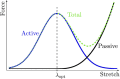
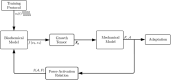
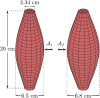
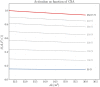
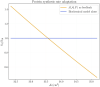
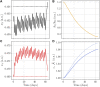
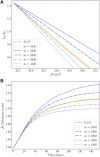
Skeletal muscle adaptation is correlated to training exercise by triggering different signaling pathways that target many functions; in particular, the IGF1-AKT pathway controls protein synthesis and degradation. These two functions regulate the adaptation in size and strength of muscles. Computational models for muscle adaptation have focused on: the biochemical description of signaling pathways or the mechanical description of muscle function at organ scale; however, an interrelation between these two models should be considered to understand how an adaptation in muscle size affects the protein synthesis rate. In this research, a dynamical model for the IGF1-AKT signaling pathway is linked to a continuum-mechanical model describing the active and passive mechanical response of a muscle; this model is used to study the impact of the adaptive muscle geometry on the protein synthesis at the fiber scale. This new computational model links the signaling pathway to the mechanical response by introducing a growth tensor, and links the mechanical response to the signaling pathway through the evolution of the protein synthesis rate. The predicted increase in cross sectional area (CSA) due to an 8 weeks training protocol excellently agreed with experimental data. Further, our results show that muscle growth rate decreases, if the correlation between protein synthesis and CSA is negative. The outcome of this study suggests that multi-scale models coupling continuum mechanical properties and molecular functions may improve muscular therapies and training protocols.

Keywords: biochemical modeling; biomechanics; cellular signaling pathways; dynamical systems; mechanobiology; muscle adaptation; population dynamics.

FIGURE 1

Simplified signaling pathway for muscle adaptation presented by Schiaffino and Mammucari (2011). IGF1 activates AKT, AKT activates mTOR and inhibits FOXO, FOXO inhibits mTOR and promotes atrophy, mTOR promotes hypertrophy.

FIGURE 2

Force-Stretch relation for a muscle. λ _opt is the stretch where the muscle exerts its maximum force, decreasing or increasing stretch will produce a drop in the generated force. During active response, the maximum isometric tension σ _o characterizes the maximum force, and the active stretch λ _a characterizes stretch; whereas during passive response, the stretch of collagen fibers ${\overline{I}}_4$ characterizes stretch.

FIGURE 3

Algorithm for the mechanobiological model for muscle adaptation. Each function outside a block is an output of the closer block and an input for the next block. f is the rate of change of the myofibril population, F _g is the growth tensor, F and $\mathcal{A}$ are the force and CSA of the updated muscle structure, and $\beta (\mathcal{A},F)$ is the inverse function of the force-activation relation at CSA $\mathcal{A}$ .

FIGURE 4

Comparison between muscle structure before and after the training protocol.

FIGURE 5

Cross Sectional Area and myofibril population comparison. These results were obtained by considering full activation (β = 1) for the whole training protocol, and no feedback from the mechanical to the biochemical model.

FIGURE 6

Activation level β as a function of the CSA $\mathcal{A}$ for different force levels. The activation required to produce a fixed force decreases as the CSA of the structure increases. Each curve results by fixing the value of F and calculating β according to Supplementary Equations S24, S25.

FIGURE 7

Protein synthesis rate k ₁ given by Eq. 15, at parameters d ₁ = 20.40 and d ₂ = 18.907. Here, we compare the growth rate k ₁ of the original biochemical system Eqs 1a, 1b, 1c, 1d, 1e with the modified value of k ₁ using the feedback from the mechanical response.

FIGURE 8

Normalized CSA adaptation due to training. Experimental results compared to our mechanobiological model. The activation function shown in Figure 6 was used to feedback equation system Eqs 1a, 1b, 1c, 1d, 1e. The modified protein synthesis rate k ₁(β) was defined in Eq. 15, and replaces the constant value of the protein synthesis rate in function $f\left(x_3,x_4\right)$ defined through Eq. 2. We simulated the training protocol of DeFreitas et al. (2011), and fitted parameters d ₁ and d ₂ to minimize the RMSE.

FIGURE 9

Biochemical variables and protein synthesis rate during the CSA adaptation shown in Figure 8. Dashed lines represent threshold levels in figures (A,C); these figures show that periodic training leads to oscillations of x ₃ below its threshold, and x ₄ above its threshold; those levels favor hypertrophy according to Eq. 2. Figures (B,D) show that protein synthesis rate decreases as z increases. And figure (D) shows the results presented in Figure 5 after the use of function $\beta (\mathcal{A},F)$ as feedback; recall that the elastic response required for compatible configuration explains the difference between z (continuous line) and $\widehat{\mathcal{A}}$ (dotted line). (a.u., arbitrary units).

FIGURE 10

CSA increase under variation of: (A) training frequency, and (B) the proportionality constant κ defined in Supplementary Equation S16, with ${\kappa }_0=1/\mathcal{A}(0)$ .

FIGURE 11

(A) is the linear approximation of the k ₁/k ₁₀ numerical solution of Figure 7, the variation of the slope represents different protein synthesis responses. (B) Evolution of the CSA for the different variations presented in (A).