Topological gelation of reconnecting polymers

Abstract

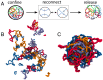
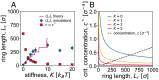
DNA recombination is a ubiquitous process that ensures genetic diversity. Contrary to textbook pictures, DNA recombination, as well as generic DNA translocations, occurs in a confined and highly entangled environment. Inspired by this observation, here, we investigate a solution of semiflexible polymer rings undergoing generic cutting and reconnection operations under spherical confinement. Our setup may be realized using engineered DNA in the presence of recombinase proteins or by considering micelle-like components able to form living (or reversibly breakable) polymer rings. We find that in such systems, there is a topological gelation transition, which can be triggered by increasing either the stiffness or the concentration of the rings. Flexible or dilute polymers break into an ensemble of short, unlinked, and segregated rings, whereas sufficiently stiff or dense polymers self-assemble into a network of long, linked, and mixed loops, many of which are knotted. We predict that the two phases should behave qualitatively differently in elution experiments monitoring the escape dynamics from a permeabilized container. Besides shedding some light on the biophysics and topology of genomes undergoing DNA reconnection in vivo, our findings could be leveraged in vitro to design polymeric complex fluids-e.g., DNA-based complex fluids or living polymer networks-with desired topologies.

Keywords: DNA topology; MD simulations; living polymers; topological gel.

Fig. 1.

Phases of reconnecting rings. (A) We study ring polymers allowed to recombine/reconnect within a sphere of radius R. (B and C) The two panels show two possible states of the system at equilibrium and after relaxing the confinement. B is a sketch of an ensemble of many, small, and mostly unlinked rings, whereas C shows an ensemble of few, long, and linked rings. The snapshots are taken after releasing confinement for ease of visualization.

Fig. 2.

Geometrical transition of reconnecting rings. (A and B) Time evolution of the average number (n.) of reconnecting rings N_r (A) and their average contour length L_r (B). Different curves refer to different values of the stiffness parameter K. All the data refer to a spherical confinement of radius $R=7\sigma$. (C and D) Average steady-state values of $\langle N_r\rangle$ and $\langle L_r\rangle$, respectively, as a function of K. The black line in C and C, Inset shows the theoretical prediction from Eq. 1 with $\lambda =5.3$ and a = 0.27. (E and F) Distributions of ring size in steady state, for K = 1 (E) and K = 5 (F), indicating that the system is always highly polydisperse. (G) Probability that a ring of length L_r mixes with other rings as a function of L_r, for different values of K. (H) Heatmap of the radial distribution (G(r)) of monomers in rings of length L_r as a function of r, the distance from the center of the confinement sphere, and L_r.

Fig. 3.

Critical point for gelation. (A) Filled squares: critical length $L^{*}$, for which the concentration c of a ring in a sphere with $R=7\sigma$ equals $c^{*}$, as a function of K. Filled circles: mean ring length versus K. The critical point for gelation is expected to be where the two curves cross. (B) Calculation of $L^{*}$. At $L^{*}$, the curves ($c^{*}$ as a function of K) and the dotted line (c as a function of K) intersect. $c^{*}$ is predicted for an ideal polymer ring (Eq. 2). Crit., critical.

Fig. 4.

Topological gelation. (A and B) Time dependence of the number of linked pairs of rings N_Lk (A) and average of the total unsigned linking number, $\langle \left|Lk\right|\rangle$, (B). Different curves refer to different values of the stiffness parameter K. (C and D) Average steady-state values of N_Lk and $\langle \left|Lk\right|\rangle$, respectively, as a function of K. (E and F) Probability of observing a single cluster as a function of K (E) and as a function of the linking probability (F). (G) Examples of knots and catenanes found in the steady-state configurations at K = 5. (H) Snapshots of clusters of linked rings in simulations with K = 1 and K = 5. Each sampled configuration is associated with a network; linked rings (vertices) are connected by edges. A connected component of the network represents a cluster of linked rings. Av., average; n., number; pr., probability; tot., total.

Fig. 5.

Escape dynamics of reconnecting rings from a permeabilized sphere. Results of simulated elution experiments from a permeabilized sphere. The different structures correspond to a system of reconnecting rings with different K. After permeabilizing the sphere, K was set to 1 for all systems, and the reconnection was disallowed, in order to focus on the effect of topology on the escape dynamics. (Left) Number of monomers inside the sphere as a function of time for an initial value of K equal to 0 (A) and 3 (B). Corresponding snapshots are shown in Right (with and without the sphere to ease visualization of the topological structures). Simulations are performed inside a box with periodic boundaries.