Modular pulse synthesizer for transcranial magnetic stimulation with fully adjustable pulse shape and sequence
- PMID: 36301685
- PMCID: PMC10206176
- DOI: 10.1088/1741-2552/ac9d65
Modular pulse synthesizer for transcranial magnetic stimulation with fully adjustable pulse shape and sequence
Abstract
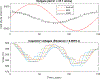
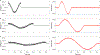
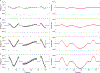
The temporal shape of a pulse in transcranial magnetic stimulation (TMS) influences which neuron populations are activated preferentially as well as the strength and even direction of neuromodulation effects. Furthermore, various pulse shapes differ in their efficiency, coil heating, sensory perception, and clicking sound. However, the available TMS pulse shape repertoire is still very limited to a few biphasic, monophasic, and polyphasic pulses with sinusoidal or near-rectangular shapes. Monophasic pulses, though found to be more selective and stronger in neuromodulation, are generated inefficiently and therefore only available in simple low-frequency repetitive protocols. Despite a strong interest to exploit the temporal effects of TMS pulse shapes and pulse sequences, waveform control is relatively inflexible and only possible parametrically within certain limits. Previously proposed approaches for flexible pulse shape control, such as through power electronic inverters, have significant limitations: The semiconductor switches can fail under the immense electrical stress associated with free pulse shaping, and most conventional power inverter topologies are incapable of generating smooth electric fields or existing pulse shapes. Leveraging intensive preliminary work on modular power electronics, we present a modular pulse synthesizer (MPS) technology that can, for the first time, flexibly generate high-power TMS pulses (one-side peak ∼4000 V, ∼8000 A) with user-defined electric field shape as well as rapid sequences of pulses with high output quality. The circuit topology breaks the problem of simultaneous high power and switching speed into smaller, manageable portions, distributed across several identical modules. In consequence, the MPS TMS techology can use semiconductor devices with voltage and current ratings lower than the overall pulse voltage and distribute the overall switching of several hundred kilohertz among multiple transistors. MPS TMS can synthesize practically any pulse shape, including conventional ones, with fine quantization of the induced electric field (⩽17% granularity without modulation and ∼300 kHz bandwidth). Moreover, the technology allows optional symmetric differential coil driving so that the average electric potential of the coil, in contrast to conventional TMS devices, stays constant to prevent capacitive artifacts in sensitive recording amplifiers, such as electroencephalography. MPS TMS can enable the optimization of stimulation paradigms for more sophisticated probing of brain function as well as stronger and more selective neuromodulation, further expanding the parameter space available to users.
Keywords: activation selectivity; arbitrary waveform generation; electric field quantization; flexible pulse shape synthesis; pulse sequence control; temporal control flexibility; transcranial magnetic stimulation.
© 2022 IOP Publishing Ltd.
Figures










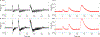



Similar articles
-
Optimized monophasic pulses with equivalent electric field for rapid-rate transcranial magnetic stimulation.J Neural Eng. 2023 Jun 6;20(3):10.1088/1741-2552/acd081. doi: 10.1088/1741-2552/acd081. J Neural Eng. 2023. PMID: 37100051 Free PMC article.
-
Modular multilevel TMS device with wide output range and ultrabrief pulse capability for sound reduction.J Neural Eng. 2022 Mar 17;19(2):10.1088/1741-2552/ac572c. doi: 10.1088/1741-2552/ac572c. J Neural Eng. 2022. PMID: 35189604 Free PMC article.
-
An Efficient Pulse Circuit Design for Magnetic Stimulation with Diversified Waveforms and Adjustable Parameters.Sensors (Basel). 2024 Jun 13;24(12):3839. doi: 10.3390/s24123839. Sensors (Basel). 2024. PMID: 38931623 Free PMC article.
-
The development and modelling of devices and paradigms for transcranial magnetic stimulation.Int Rev Psychiatry. 2017 Apr;29(2):115-145. doi: 10.1080/09540261.2017.1305949. Epub 2017 Apr 26. Int Rev Psychiatry. 2017. PMID: 28443696 Free PMC article. Review.
-
TMS-EEG: A window into the neurophysiological effects of transcranial electrical stimulation in non-motor brain regions.Neurosci Biobehav Rev. 2016 May;64:175-84. doi: 10.1016/j.neubiorev.2016.03.006. Epub 2016 Mar 6. Neurosci Biobehav Rev. 2016. PMID: 26959337 Review.
Cited by
-
A novel pulse-current waveform circuit for low-energy consumption and low-noise transcranial magnetic stimulation.Front Neurosci. 2025 Jan 7;18:1500619. doi: 10.3389/fnins.2024.1500619. eCollection 2024. Front Neurosci. 2025. PMID: 39840017 Free PMC article.
-
Optimized monophasic pulses with equivalent electric field for rapid-rate transcranial magnetic stimulation.J Neural Eng. 2023 Jun 6;20(3):10.1088/1741-2552/acd081. doi: 10.1088/1741-2552/acd081. J Neural Eng. 2023. PMID: 37100051 Free PMC article.
-
The complex landscape of TMS devices: A brief overview.PLoS One. 2023 Nov 28;18(11):e0292733. doi: 10.1371/journal.pone.0292733. eCollection 2023. PLoS One. 2023. PMID: 38015924 Free PMC article.
-
xTMS: A Pulse Generator for Exploring Transcranial Magnetic Stimulation Therapies.Conf Proc (IEEE Appl Power Electron Conf Expo). 2023 May 31;2023:1875-1880. doi: 10.1109/APEC43580.2023.10131554. Conf Proc (IEEE Appl Power Electron Conf Expo). 2023. PMID: 37342241 Free PMC article.
-
Closed-loop optimal and automatic tuning of pulse amplitude and width in EMG-guided controllable transcranial magnetic stimulation.Biomed Eng Lett. 2022 Dec 30;13(2):119-127. doi: 10.1007/s13534-022-00259-3. eCollection 2023 May. Biomed Eng Lett. 2022. PMID: 37124104 Free PMC article.
References
-
- Rossini PM, Burke D, Chen R, Cohen LG, Daskalakis Z, Di Iorio R, et al., “Non-invasive electrical and magnetic stimulation of the brain, spinal cord, roots and peripheral nerves: Basic principles and procedures for routine clinical and research application. An updated report from an I.F.C.N. Committee,” Clinical Neurophysiology, vol. 126, pp. 1071–1107, 2015. - PMC - PubMed
-
- Barker AT, Jalinous R, and Freeston IL, “Non-invasive magnetic stimulation of human motor cortex,” The Lancet, vol. 325, pp. 1106–1107, 1985. - PubMed
-
- Nardone R, Höller Y, Taylor A, Thomschewski A, Orioli A, Frey V, et al., “Noninvasive Spinal Cord Stimulation: Technical Aspects and Therapeutic Applications,” Neuromodulation: Technology at the Neural Interface, vol. 18, pp. 580–591, 2015. - PubMed
-
- Polson MJR, Barker AT, and Freeston IL, “Stimulation of nerve trunks with time-varying magnetic fields,” Medical and Biological Engineering and Computing, vol. 20, pp. 243–244, 1982. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
