A Bayesian model for chronic pain

Abstract

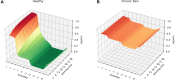
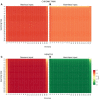
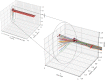
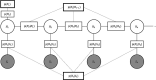
The perceiving mind constructs our coherent and embodied experience of the world from noisy, ambiguous and multi-modal sensory information. In this paper, we adopt the perspective that the experience of pain may similarly be the result of a probabilistic, inferential process. Prior beliefs about pain, learned from past experiences, are combined with incoming sensory information in a Bayesian manner to give rise to pain perception. Chronic pain emerges when prior beliefs and likelihoods are biased towards inferring pain from a wide range of sensory data that would otherwise be perceived as harmless. We present a computational model of interoceptive inference and pain experience. It is based on a Bayesian graphical network which comprises a hidden layer, representing the inferred pain state; and an observable layer, representing current sensory information. Within the hidden layer, pain states are inferred from a combination of priors $p\left(\text{pain}\right)$ , transition probabilities between hidden states $p({\text{pain}}_{t+1}\mid {\text{pain}}_t)$ and likelihoods of certain observations $p(\text{sensation}\mid \text{pain})$ . Using variational inference and free-energy minimization, the model is able to learn from observations over time. By systematically manipulating parameter settings, we demonstrate that the model is capable of reproducing key features of both healthy- and chronic pain experience. Drawing on mathematical concepts, we finally simulate treatment resistant chronic pain and discuss mathematically informed treatment options.

Keywords: Bayesian inference; belief-propagation; chronic pain; computational psychiatry; free energy; graphical models; interoception; predictive coding.

Figure 1

Bayesian network representation of pain perception. We model perception in time as a hidden Markov model, where unobservable (hidden) nodes $H_t$ form a Markov chain. These hidden nodes represent the state of the body, that the perceiving agent has no direct access to. Each hidden node connects to an observable node $S_t$, which represents a sensory (e.g. noxious) input. The connections indicate the direction of causation: body states cause noxious inputs in a healthy agent. Tables show exemplary settings of relevant probabilities for both healthy and chronic pain perception, where prior probabilities are chosen so that expectations are stable in time (see Appendix B for details).

Figure 2

Healthy (A) and chronified pain inference (B). The $X$-axis shows the time-step, referring to e.g. times during a day. The learning trials on the $Z$-axis refer to moments of parameter updates, e.g. consecutive days, or longer-term memory consolidation and learning. On the $Y$-axis, the inferred marginal probabilities of pain are represented. Both models were exposed to noxious sensory information at nodes 1–5, and to harmless sensory information at nodes 12–18 for 40 learning trials. The inferred marginal probabilities develop dynamically in the case of healthy inference (left), whereas there are hardly any deviations from the prior beliefs in the case of chronified pain inference (right).

Figure 3

Effect of prolonged exposure to one type of information. The $X$-axis in all plots shows the time step (e.g., time steps during a day), and the $Y$-axis shows learning trials (e.g., memory consolidation at the end of each day). (A) and (B) show the observer with chronic pain exposed to 20 time steps and 40 trials of noxious information (A), and 20 time steps and 40 trials of harmless observations (B). (C) and (D) illustrate the same observational scheme under healthy pain inference. Of note, the marginal probabilities inferred at the first- and last time step differ from the probabilities inferred in intermittent nodes for two reasons. First, due to our model architecture, the first- and final nodes only receive messages related to sensory inputs from one neighbour, while intermittent nodes receive richer sensory information from their two respective neighbours (e.g., past and future time steps), leading to increased certainty about the hidden state. Secondly, we perform batch updates at the end of one time series. In psychological terms, this corresponds to retrospective memory consolidation during sleep. With increased learning trials ($Y$-axis), however, the marginal probability of inferring pain under noxious stimulation (panels A and C) increases as a consequence of learning.

Figure 4

Null space of deviations from final state: over time, the marginal probability of inferring pain approaches and stabilizes within ranges of the preset marginal, here, $p(pain)=0.7$. Random changes to the prior expectation of pain (at time step 0, illustrated by the different-colour lines) are overridden within two time steps, and the marginal probability approaches the predefined value.

Figure 5

Simulation of ten sessions of exposure therapy in the nullspace of marginal $p(pain)=0.7$, with ambiguous and imprecise likelihoods (A) and precise and accurate likelihoods (B). On the $X$-axis are the time steps, on the $Y$-axis the marginal probabilities of pain, and on the $Z$-axis the learning trials per time step. The combination of null space derived transition probabilities and an imprecise and ambiguous likelihood model ($p(\text{noxious}\mid \text{pain})=0.6$, $p(\text{harmless}\mid \text{pain})=0.4$, $p(\text{noxious}\mid \overline{\text{pain}})=0.6$, $p(\text{harmless}\mid \overline{\text{pain}})=0.4$) renders the repeated presentation of innocuous sensory information rather inefficient: inferred probabilities of pain remain within the range of the predefined marginal. When the likelihood model is precise and unambiguous ($p(\text{noxious}\mid \text{pain})=0.8$, $p(\text{harmless}\mid \text{pain})=0.2$, $p(\text{noxious}\mid \overline{\text{pain}})=0.1$, $p(\text{harmless}\mid \overline{\text{pain}})=0.9$), however, the presentation of harmless sensory information is more efficient in reducing the inferred probability of pain.

Figure 6

Tabular overview of patient experience and model predictions. Timepoints: T $\pm$ month, Model parameters: expected pattern of change in the model parameters underlying chronic vs. acute pain experience; where $p$, pain; $\overline{p}$, pain-free state; $n$, noxious input; $\overline{n}$, harmless input. Self-report: Expected values, $\uparrow$, increased values compared to baseline; $\downarrow$, decreasing values; $\to$, average values; *, there is some evidence that the generative model of patients with chronic pain is biased towards pain from childhood on, e.g. via traumatic experiences, abuse and earlier chronic pain experiences (–70).

Figure A1

Graphical model (fragment). Graphical model depicting the inter-dependencies between hidden $H_t$ and observable $S_t$ variables. Connected to each variable node, factor nodes are necessary to perform variational inference message passing. This approach is computationally efficient because it allows message passing without re-instantiating the model at each time-step. The observable nodes $S_t$ represent incoming sensory information, $S\in \{\text{noxious}(1),\text{harmless}(0)\}$. The hidden states, representing the system’s internal model, can in turn take on the values 0 (no pain) or 1 (pain), or $H\in \{\text{pain},\overline{\text{pain}}\}$. The likelihood $p(S_t\mid H_t)$ is the top-down factor in this model and allows quantifying the association between the model’s state $H_t$ and the observed sensory input at $S_t$. The hidden variable nodes form a Markov chain and contain transition probabilities $p(H_t\mid H_{t+1})$, which can be interpreted as the development of the pain prior over time. In individuals with chronic pain, we here assume that $p(H_t=\text{pain}\mid H_{t-1}=\text{pain})>p(H_t=\overline{\text{pain}}\mid H_{t-1}=\text{pain})$.

Figure B1

Illustration of null space of transition probability deviations for different marginal $p({\text{pain}}_{\mathrm{\infty }})$. We show that when the transition probabilities $p({\text{pain}}_{t+1}\mid {\text{pain}}_t)$ and $p({\overline{\text{pain}}}_{t+1}\mid {\overline{\text{pain}}}_t)$ are sampled from the one-dimensional null space of a given marginal probability of pain $p({\text{pain}}_{\mathrm{\infty }})$, the marginal probability $p({\text{pain}}_t)$ will approach and stabilize within the range of $p({\text{pain}}_{\mathrm{\infty }})$. Here, we illustrate the transition probabilities for $p({\text{pain}}_{\mathrm{\infty }})\in [0.1,0.9]$ (legend).