Reaction-diffusion models in weighted and directed connectomes
- PMID: 36306284
- PMCID: PMC9683624
- DOI: 10.1371/journal.pcbi.1010507
Reaction-diffusion models in weighted and directed connectomes
Abstract
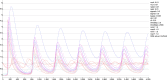
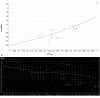
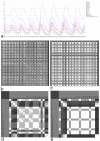
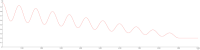
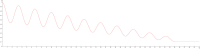
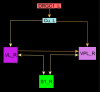
Connectomes represent comprehensive descriptions of neural connections in a nervous system to better understand and model central brain function and peripheral processing of afferent and efferent neural signals. Connectomes can be considered as a distinctive and necessary structural component alongside glial, vascular, neurochemical, and metabolic networks of the nervous systems of higher organisms that are required for the control of body functions and interaction with the environment. They are carriers of functional phenomena such as planning behavior and cognition, which are based on the processing of highly dynamic neural signaling patterns. In this study, we examine more detailed connectomes with edge weighting and orientation properties, in which reciprocal neuronal connections are also considered. Diffusion processes are a further necessary condition for generating dynamic bioelectric patterns in connectomes. Based on our precise connectome data, we investigate different diffusion-reaction models to study the propagation of dynamic concentration patterns in control and lesioned connectomes. Therefore, differential equations for modeling diffusion were combined with well-known reaction terms to allow the use of connection weights, connectivity orientation and spatial distances. Three reaction-diffusion systems Gray-Scott, Gierer-Meinhardt and Mimura-Murray were investigated. For this purpose, implicit solvers were implemented in a numerically stable reaction-diffusion system within the framework of neuroVIISAS. The implemented reaction-diffusion systems were applied to a subconnectome which shapes the mechanosensitive pathway that is strongly affected in the multiple sclerosis demyelination disease. It was found that demyelination modeling by connectivity weight modulation changes the oscillations of the target region, i.e. the primary somatosensory cortex, of the mechanosensitive pathway. In conclusion, a new application of reaction-diffusion systems to weighted and directed connectomes has been realized. Because the implementation was realized in the neuroVIISAS framework many possibilities for the study of dynamic reaction-diffusion processes in empirical connectomes as well as specific randomized network models are available now.
Copyright: © 2022 Schmitt et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

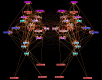






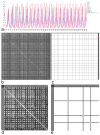


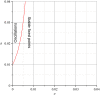

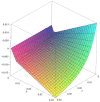
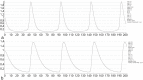


References
-
- Turing AM. The chemical basis of morphogenesis. Phil Trans R Soc Lond B. 1952; 237: 37–72. doi: 10.1098/rstb.1952.0012 - DOI
-
- Prigogine I, Lefever R. Symmetry breaking instabilities in dissipative systems. J Chem Phys. 1968; 48: 1695–1700. doi: 10.1063/1.1668896 - DOI
-
- Ouyang Q, Swinney HL. Transition from an uniform state to hexagonal and striped Turing patterns. Nature 1991; 352: 610–612. doi: 10.1038/352610a0 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

